1. Searching for Solutions
Nel caso più semplice in cui un agente può trovarsi, questo conosce un modello perfetto del mondo senza incertezze, e un solo goal da perseguire. Il problema può essere astratto alla ricerca di un percorso in un grafo orientato da un nodo di partenza a un nodo goal. Quando un agente riceve il problema, riceve solo una descrizione di cosa rappresenti una soluzione, e deve provvedere a trovare una soluzione a problemi che magari sono difficili anche per gli uomini, per cui ci si accontenta alcune volte di soluzioni soddisfacenti, oppure si utilizza della conoscenza aggiuntiva (euristica).
1 Spazi di stati
Uno stato contiene tutta l’informazione necessaria a predire gli effetti di un’azione e verificare se soddisfa il goal. Gli spazi di stati assumono che:
L’agente ha una conoscenza perfetta dello spazio.
In ogni momento, sa in che stato si trova (mondo completamente osservabile)
L’agente ha un insieme di azioni dagli effetti deterministici noti.
L’agente ha un goal da perseguire e sa determinare quale stato soddisfa il goal
Un problema di ricerca comprende:
uno spazio di stati
uno stato di partenza
per ogni stato, un set di azioni ammesse
una funzione d’azione: (stato, azione) -> nuovo stato
un obiettivo rappresentato da una funzione booleana goal(s) vera quando lo stato s soddisfa il goal (s: goal state)
un criterio di qualità per le soluzioni accettabili, per esempio qualsiasi soluzione può essere accettata, oppure se vi sono costi associati alle azioni magari si vuole minimizzare tale costo. La miglior soluzione basata su questi criteri è definita soluzione ottimale
2 Algoritmo di ricerca generico
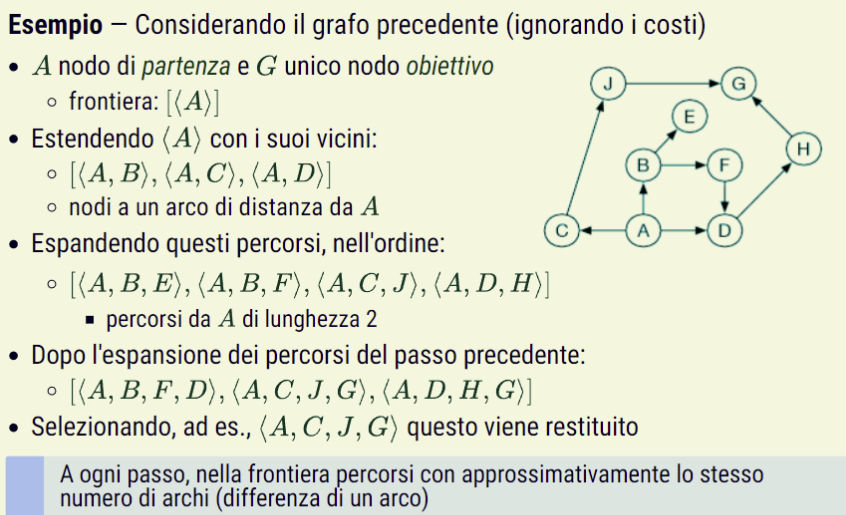
Dato un grafo, un nodo di partenza, e un nodo goal, si esplorano incrementalmente percorsi dai nodi di partenza verso nodi-obiettivo. Questo viene fatto mantenendo una frontiera di percorsi dal nodo di partenza. La frontiera contiene tutti i percorsi visitati dal nodo di partenza al nodo goal. Inizialmente, la frontiera contiene il percorso costituito dal solo nodo di partenza, successivamente questo percorso viene espanso verso nodi inesplorati, fino a incontrare il nodo goal. Ad ogni passo si seleziona un percorso rimuovendolo dalla frontiera, lo si estende con ogni arco uscente dall’ultimo nodo e si aggiungono alla frontiera i percorsi ottenuti:

Quale percorso viene selezionato nel ciclo definisce la strategia di ricerca. La selezione di un percorso ha un impatto sull’efficienza
Il return dell’if può essere visto come un return temporaneo, ovvero si può continuare il while anche dopo essere finiti in quell’if per cercare strade alternative
Se la procedura ritorna ⊥ non ci sono altre soluzioni.
L’algoritmo testa se un percorso termina in un nodo goal dopo che il percorso è stato scelto dalla frontiera e non quando viene aggiunto. Questo perché a volte esiste un arco verso un nodo goal con un costo elevato, mentre potrebbe comunque esserci un percorso di costo inferiore, e la verifica stessa se un nodo è goal può essere costosa.
3 Strategie di ricerche non informate
Le strategie non informate sono quelle strategie che non prendono in considerazione la posizione dell’obiettivo.
- Ricerca in ampiezza (BFS): la frontiera è implementata con una coda, si seleziona il primo percorso aggiunto e ad ogni passo si seleziona uno dei percorsi più corti.
| Utile | Inutile |
|---|---|
| Se non ho problemi di spazio | Grafo generato dinamicamente (complessità in spazio) |
| Se si cerca una soluzione con numero di archi minimale | Soluzioni con percorsi molto lunghi |
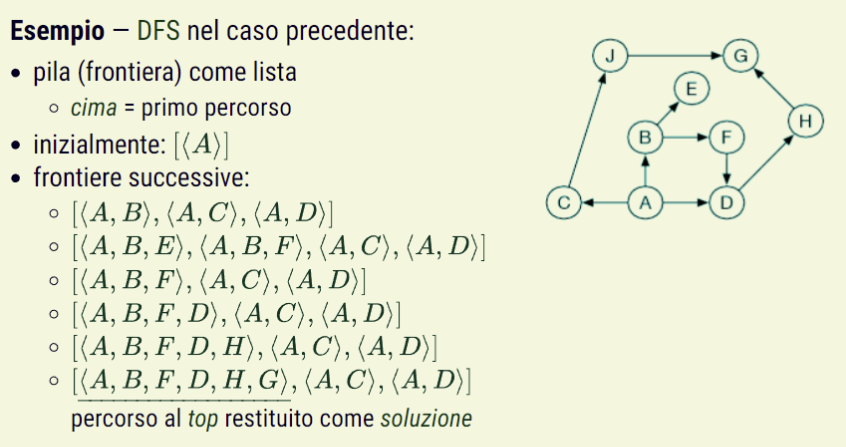
Ricerca in profondità (DFS): la frontiera è implementata come una pila, quindi si completa un singolo percorso prima di provare alternative (backtracking: si seleziona una prima alternativa per ogni nodo, tornando indietro alla successiva solo dopo aver tentato tutti i completamenti).
- L’algoritmo non specifica in che ordine i percorsi vanno aggiunti alla frontiera, quindi l’efficienza dipende dall’ordine con cui i vicini dell’ultimo nodo vengono espansi.
| Utile | Inutile |
|---|---|
| Limitazioni di spazio | Percorsi infiniti (cicli o grafo infinito) |
| Diventa ideale se tutti i percorsi portano a soluzione o se l’ordine di aggiunta dei vicini può essere variato in modo da trovare la soluzione al primo tentativo senza backtracking | Ricerca si attarda su percorsi più lunghi pure avendo alternative poco profonde |
Iterative Deepening: l’algoritmo combina l’efficienza in spazio della DFS con l’ottimalità della BFS. L’idea è quella di computare ogni volta tutti gli elementi di una frontiera rispetto a memorizzarli. Ogni computazione può essere una DFS, che occupa meno spazio. Si utilizza quindi una DFS fino a una profondità-limite per le iterazioni in BFS, in sostanza opero una visita in ampiezza per ogni livello di profondità.
La soluzione con il minor numero di archi sarà individuata per prima
L’algoritmo fallisce se raggiunge il limite di profondità imposto per quella iterazione (fallimento innaturale) o se esaurisce lo spazio di ricerca (fallimento naturale). Nel primo caso basta riprovare con una profondità maggiore, nel secondo caso invece non ci sono percorsi per raggiungere il nodo goal.



Ricerca a costo minimo: se gli archi non hanno costi unitari si cerca la soluzione di minimo costo totale.
- Lowest-cost-first search: simile alla BFS, ma invece di espandere il percorso con il minor numero di archi, seleziona il percorso col costo minore. La frontiera viene implementata con una coda con priorità ordinata sulla base del costo di ogni percorso.

4 Strategie di ricerca informate
4.1 Ricerca euristica
Una funzione euristica h(n) prende un nodo n e ritorna un numero positivo che rappresenta la stima del costo del percorso meno costoso da n al nodo goal.
h(n) è una euristica ammissibile se sottostima il costo reale del percorso da n a goal. Se una funzione è una euristica ammissibile allora, utilizzando determinati teoremi, possiamo dimostrare che ci darà una soluzione corretta, altrimenti l’algoritmo potrebbe anche non terminare.
Un semplice utilizzo della funzione euristica sulla DFS è il seguente: aggiungo i vicini nella pila in modo che il miglior vicino sia selezionato per primo, quindi aggiungo i vicini in ordine dall’euristica più alta alla più bassa, in modo da estrarre per primo quest’ultimo. E’ un approccio greedy poichè seleziona sempre il miglior percorso locale, ma esplora tutti i percorsi che estendono quello selezionato prima di tentarne altri. Soffre dei problemi della DFS, quindi non garantisce di trovare una soluzione e potrebbe non trovare una soluzione ottimale.
Un altro utilizzo è quello della greedy best-first search: è una lowest-cost-first search in cui seleziono il percorso con h(n) minore (nella LCFS sceglievo il percorso con costo minore). Potrebbe seguire percorsi promettenti che però potrebbero continuare a estendersi indefinitamente.
4.2 A^{\star} Search
A^{\star} cerca il percorso col costo minore e sfrutta l’euristica per migliorare la ricerca, utilizza sia il costo del percorso come nella lowest-cost-first, e sia la funzione euristica, come nella greedy-best-first search, per scegliere il percorso da espandere. Per ogni percorso p nella frontiera, A* stima il costo dell’intero percorso fino al nodo goal usando sia il costo del percorso che la funzione euristica: f(p) = cost(p) + ℎ(p).
A^{\star} è implementato usando l’algoritmo di ricerca generico, trattando la frontiera come una priority queue con sort su f(p).
A^{\star} è ammissibile (= trova sempre la soluzione ottimale) se il fattore di ramificazione è limitato, il costo degli archi è maggiore di un certo \epsilon > 0 e se h(n) è una euristica ammissibile, così che f(p) non sovrastimerà mai il costo del percorso per andare dal nodo start al nodo goal passando per p.
L’ammissibilità non assicura che i nodi intermedi selezionati dalla frontiera siano un cammino ottimo, ma assicura che la prima soluzione sarà ottimale anche in presenza di cicli.
In presenza di cicli il costo del percorso in cui il ciclo è coinvolto salirà, e quindi prima o poi l’A^{\star} smetterà di seguire quel percorso.
4.3 Branch and Bound
Combina l’efficienza in spazio delle strategie in profondità con l’euristica, in particolare è molto efficace quando esistono molti cammini verso un goal, e assumendo che h(n) è ammissibile. L’idea è quella di mantenere il percorso di costo minimo verso un goal trovato e il suo costo che diventa un bound: se la ricerca trova un path p tale che cost(p) + h(p) \geq bound, allora il percorso p può essere scartato, altrimenti il percorso trovato è quello ottimale fino ad ora e quindi si aggiorna bound e si continua a cercare, migliorando via via il risultato.
Viene implementata in maniera simile alla depth-bounded search, dove il bound è in termini di costo del percorso.

Inizialmente, il bound può essere settato a \infty o come una sovrastima. L’algoritmo ritornerà una soluzione ottimale se vi è una soluzione con un costo minore del bound impostato, quindi l’algoritmo può essere utilizzato anche in presenza di constraint particolari riguardo il costo del percorso.
Se l’algoritmo non trova soluzioni, in caso di bound iniziale infinito non vi sono soluzioni globali, in caso di bound finito non vi sono soluzioni locali.
Combinato con ID può incrementare il limite, in caso questo sia stato settato, fino a trovare una soluzione, se esiste.
Rispetto all’A^{\star} non sviluppa gli archi che superano il costo minimo già trovato per un percorso.
4.4 Progettare la funzione euristica
Il modo standard per definire un’euristica è quella di trovare una soluzione di un problema più semplice con meno vincoli: una soluzione ottimale per un problema più semplice è difficile che abbia un costo maggiore rispetto al costo ottimale di un problema più grande.
In molti problemi spaziali in cui il costo è la distanza e la soluzione è vincolata a percorrere archi predefiniti la distanza euclidea rettilinea tra due nodi è un’euristica ammissibile perché è la soluzione al problema più semplice in cui l’agente non è vincolato a percorrere gli archi.
Una volta semplificato, il problema può essere risolto utilizzando la ricerca, che dovrebbe essere più semplice del problema originale. Questo deve essere risolto più volte, forse anche per tutti i nodi, quindi spesso è utile memorizzare i risultati in un database di modelli che mappa i nodi del problema più semplice col valore dell’euristica. Nel problema astratto più semplice, spesso ci sono meno nodi, con più nodi originali mappati in un singolo nodo del grafo semplificato, il che può rendere feasible la memorizzazione del valore euristico per ciascun nodo.
4.5 Potatura dello spazio di ricerca
Gli algoritmi precedenti possono essere migliorati prendendo in considerazione i diversi percorsi possibili partendo da un nodo, attraverso strategie di potatura.
4.5.1 Cycle Pruning
Alcuni dei metodi visti potrebbero rimanere intrappolati in cicli. Un metodo che ci garantisca soluzione con grafi finiti consiste nel non prendere in considerazione vicini già contenuti nel percorso. In pratica, col cycle pruning, controlliamo se l’ultimo nodo del percorso è già apparso nel percorso, in caso affermativo non aggiungiamo il percorso alla frontiera.
Per metodi depth-first la complessità è costante usando un bit associato a ogni nodo, acceso quando viene aggiunto a un percorso e spento in caso di backtracking; funziona perchè si lavora su un unico percorso. In alternativa si può usare una funzione di hash.
Per le altre strategie con più percorsi (complessità in spazio esponenziale) la complessità è lineare nella lunghezza del percorso corrente: questi algoritmi non possono fare di meglio che cercare nel percorso parziale considerato, controllando che non aggiungano un nodo già presente nel percorso. #### Multiple-path Pruning Spesso più di un percorso porta a uno stesso nodo, l’idea è quella di eliminare dalla frontiera ogni percorso che porti a un nodo per il quale esiste già un altro cammino.
Il Multiple-path pruning è implementato gestendo una lista di nodi terminali di percorsi già espansi detta explored set, inizialmente vuota. Quando un percorso viene selezionato, se l’ultimo nodo è nell’explored set, il percorso viene scartato, altrimenti l’ultimo nodo viene aggiunto all’explored set e si prosegue. Per garantire di non scartare la soluzione ottimale, dato p = (s, …, n, …, m) nella frontiera, se si trova un p^{'} = (s, …, n) meno costoso si può eliminare p o sostituire in p tale parte con p^{'}.
Nella lowest-cost-first search il primo percorso verso un dato nodo è quello di costo minimo, potare altri percorsi non elimina un cammino a costo minimo per il nodo, e tagliare percorsi successivi assicura di poter trovare una soluzione ottimale.
A^{\star} non garantisce che quando si seleziona un percorso verso un nodo per la prima volta, questo sia quello di costo minimo, il teorema sull’ammissibilità lo garantisce solo per i percorsi verso il goal, per i percorsi ‘interni’ dipende dalla proprietà dell’euristica.
Una euristica consistente è una funzione h(n) non negativa che soddisfa il vincolo h(n) \leq cost(n, n^{'}) + h(n^{'}) per ogni coppia di nodi n e n^{'}. Se h(g) = 0 per ogni goal g allora h consistente non sovrastimerà mai il costo dei percorsi da un nodo verso un obiettivo. La consistenza è garantita se la relazione precedente vale anche per ogni arco (restrizione di monotonicità), ed è più facile da verificare perchè dipende dagli archi e non dalle coppie di nodi. E’ una forma di disuguaglianza triangolare: una euristica consistente è il costo stimato del cammino dal nodo n al goal non maggiore della stima di quello che obbliga al passaggio da n^{'}.
Se le condizioni sull’ammissibilità di A^{\star} sono rispettate, e l’euristica è consistente, A^{\star} con Multiple Path Pruning trova la soluzione migliore.
Di base, A^{\star} include il Multiple Path Pruning di default, andrebbe specificato il contrario.
L’MPP comprende il cycle pruning, perché un ciclo è un altro percorso verso un nodo e quindi viene potato. L’MPP può essere eseguito in tempo costante, impostando un bit su ogni nodo verso il quale è stato trovato un percorso se il grafo è memorizzato esplicitamente, oppure utilizzando una funzione hash.
L’MPP è preferibile al cycle pruning per i metodi in ampiezza, dove praticamente tutti i nodi considerati devono essere comunque memorizzati.
La ricerca in profondità non ha bisogno di memorizzare tutti i nodi alla fine dei percorsi già espansi; memorizzarli per implementare la potatura dei percorsi multipli rende la ricerca depth-first esponenziale in termini di spazio. Per questo motivo, il cycle pruning è preferito al multiple-path pruning per gli algoritmi basati sulla ricerca in profondità, incluso il branch and bound depth-first. È possibile avere un explored set di dimensioni limitate, ad esempio mantenendo solo gli elementi più recenti, il che consente una certa potatura senza l’esplosione della complessità in spazio.
5 Sommario delle strategie di ricerca
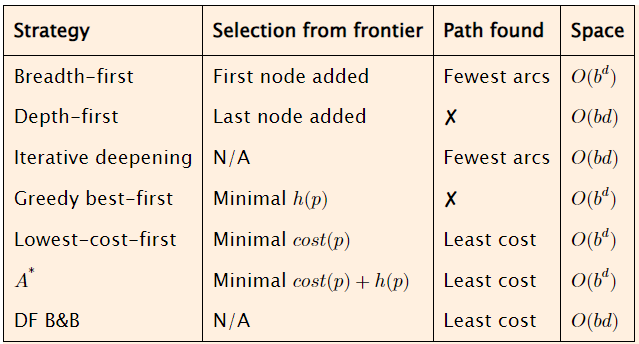
Complessità in spazio:
d profondità
b limite superiore al fattore di ramificazione
Un algoritmo di ricerca è completo se garantisce di trovare una soluzione, se ne esiste una. Sono complete quelle strategie di ricerca che garantiscono di trovare un percorso con il minor numero di archi o il minor costo. Hanno una complessità temporale nel caso peggiore che aumenta esponenzialmente con il numero di archi sui percorsi esplorati. Possono esistere algoritmi completi ma con una complessità migliore solo se P = NP, il che non dovrebbe essere vero. Gli algoritmi che non garantiscono l’halt (depth-first e greedy best-first) hanno una complessità temporale infinita nel caso peggiore.
6 Strategie di ricerca più sofisticate
6.1 Direzione della ricerca
Si potrebbe implementare una ricerca in avanti, partendo da un nodo di partenza raggiungendo i goal, oppure una ricerca all’indietro, partendo da un goal usando il grafo inverso alla ricerca del nodo di partenza, se ci sono più nodi goal viene creato un nodo goal che prendiamo come nodo di partenza e i vicini verranno inclusi nella frontiera. La direzione è indifferente se il numero di goal è infinito e se per ogni nodo si possono generare i vicini nel grafo inverso.
In alternativa si può pensare a una ricerca bidirezionale, in cui si ricostruisce il cammino quando le due frontiere si intersecano. Con la ricerca in profondità è complicato date le ridotte dimensioni delle frontiere e quindi è molto facile che percorrano lo stesso spazio. La ricerca in ampiezza garantisce l’intersezione. In generale, se si usa una DFS in una direzione, e una BFS in un’altra si garantisce l’intersezione delle frontiere di ricerca e si risparmierebbe tempo esponenziale, rimanendo però in complessità esponenziale.
Un’altra possibile strategia è la ricerca ad isole, dove si astrae il problema rimuovendo dettagli e risolvendo il problema a grana grossa, lasciando da risolvere dei sottoproblemi.
6.2 Programmazione dinamica
Un’altra proposta è l’uso della Dynamic Programming, che consiste nell’ottimizzare la soluzione memorizzando i risultati parziali, una soluzione già prodotta va ritrovata e non ricalcolata. Costruiamo una funzione cost_to_goal che da l’esatto costo di un percorso a costo minimo dal nodo di partenza al nodo goal, definita come: cost\_to\_goal(n) = \begin{cases} cost\_to\_goal(n) = 0 \; \; \text{if goal(n)} \\ min (cost(n,m) + cost\_to\_goal(m)) \; \; \text{altrimenti}\end{cases}
L’idea è di costruire una tabella di cost_to_goal(n) per ogni nodo n. Questo viene fatto usando una lowest-cost-first search con multiple-path pruning sul grafo inverso a partire dai nodi-obiettivo: si cerca il cammino di costo minimo da ogni nodo verso i goal e si conserva il valore di cost_to_goal per ogni nodo.
Si definisce una politica, ovvero quale sarà l’arco da considerare per ogni nodo. Una politica è ottimale se i suoi costi non sono mai superiori a costi di altre politiche. Data la funzione cost_to_goal, computata offline, una politica potrebbe essere computata così: partendo dal nodo n, questo dovrebbe andare al suo vicino m che minimizza cost(n, m) + cost_to_goal(m). Questa policy porta sempre a un obiettivo con un cammino di costo minimo partendo da qualsiasi nodo.
La DP può servire a costruire euristiche per A^{\star} e branch-and-bound semplificando il problema, riducendo quindi gli spazi di ricerca, e trovando in tali spazi soluzioni di lunghezza ottimale, che formeranno un database di pattern che potrebbero essere usati come euristica per il problema originale.
La DP è utile quando:
i nodi obiettivo sono espliciti
la soluzione è un cammino di costo minimo
il grafo è finito e vi è memoria per memorizzare la tabella
l’obiettivo non cambia spesso
la policy è riusabile più volte per ogni goal, ammortizzando il costo per produrre la tabella su più istanze del problema.
La criticità principale è che l’agente deve computare una nuova policy per ogni goal.