6. Supervised Machine Learning

1 Introduzione

Si parla di apprendimento supervisionato quando, dato un insieme di esempi di training descritti in termini di feature di input e feature di output, si impara a predire il valore ignoto per nuove osservazioni.

Si parla di task di classificazione quando il target è discreto (= sottoinsieme dei numeri reali), mentre si parla di regressione quando il target è continuo (= dominio infinito).

Un bias è la tendenza a preferire certe ipotesi rispetto ad altre.

2 Fondamenti

Una feature è una funzione F sugli esempi, F(e) è il valore di F per l’esempio e, il dominio della feature è l’insieme dei valori che può assumere, ossia il codominio di F.

In un task di apprendimento supervisionato, il learner riceve delle feature di input X_1, …, X_m, dei target Y_1, …, Y_k e un multiset di esempi e = (x_e, y_e) con x_e = (X_1(e), …, X_m(e)) e y_e = (Y_1(e), …, Y_k(e)). L’output è un predittore, ovvero una funzione che predice le Y basandosi sulle X. Il predittore viene costruito sugli esempi ma deve essere applicabile su tutti i possibili esempi.

3 Valutare le predizioni

Una stima puntuale di Y su un esempio e \in E è una predizione di \hat{Y} del valore di Y(e).

La loss di un esempio e su una feature Y è la misura di quanto \hat{Y}(e) è vicino al valore effettivo Y(e). Una funzione di loss comune è la mean loss, data dalla media delle loss sul numero degli esempi: \text{mean loss} = \dfrac{1}{|E|} \displaystyle \sum_{e \in E} loss(\hat{Y}, Y(e))Si potrebbe usare anche la sommatoria delle loss perchè ha lo stesso minimo della mean loss, a noi interessa minimizzarla. La mean loss viene preferita perchè il risultato è interpretabile senza conoscere il numero degli esempi.

3.1 Feature target a valori reali

Feature a valori reali sono utilizzate quando i valori sono totalmente ordinati.

Per la regressione, quando Y \in \mathbb{R} e valore attuale a e predizione p sono numeri, vengono usate le seguenti funzioni di loss:

• 0-1 loss: loss(p, a) = \begin{cases} 1 \; se\; p \neq a \\ 0 \; se\; p = a\end{cases}

  • La accuracy di un predittore è data da 1 - (mean 0-1 loss).

    • La loss media non tiene conto di quanto siano errate.

    • La accuracy è massima quando 0-1 loss è minima.

• absolute loss: loss(p, a) = |p - a|

  • il mean absolute loss è 0 solo se le predizioni corrispondono esattamente ai valori effettivi

• squared loss: loss(p, a) = (p - a)^2

  • Errore amplificato

  • Equivalentemente si può adottare la radice dell’errore quadratico medio (RMSE), poichè la radice quadrata è una funzione crescente su valori non negativi.

  • La squared loss ogni tanto si presenta con un fattore \dfrac{1}{2} davanti che rende il calcolo delle derivate più semplice

• errore nel caso pessimo: loss(E) = max |\hat{Y}(e) - Y(e)|

  • il predittore viene valutato sulla sua predizione peggiore.

3.2 Feature target categoriche

Una feature è categorica se il suo dominio è un insieme finito D = {v_1, …, v_k}.

Una stima puntuale in questo caso può essere di due tipi:

• Predizione definita di uno fra v_1, …, v_k

• Predizione probabilistica, ovvero un dizionario che mappa i valori del dominio con numeri non negativi, tale che \displaystyle \sum_{v \in D} p[v] = 1, dove p[v] è il valore della predizione p per v, quindi una sorta di peso, una probabilità che quel valore sia quello giusto.

Una predizione definita equivale a una probabilistica con p(v_j) = 1 e tutti gli altri valori associati a 0.

Le loss usate per le feature a valori reali possono essere usate anche per le feature categoriche usando loss(p[a], 1). Ad esempio, la squared loss sarebbe (1 - p[a])^2.

Le prestazioni vengono misurate con l’accuratezza media. L’accuratezza nella predizione definita è 1 se la predizione è corretta, 0 altrimenti. Nella predizione probabilistica è 1 quando c’è un’unica moda, ovvero la v con la più alta p[v] associata, che corrisponde al valore effettivo. Questa misura dipende solo dalla moda.

Una predizione probabilistica è ottimizzata usando la log loss (o categorical cross entropy): \text{logloss}(p, a) = - \log p[a]La log loss è \geq 0. E’ 0 quando p(a) = 1 e tutte le altre probabilità sono 0

Possiamo definire la log loss media: - \dfrac{1}{|Es|} \sum_e \log \hat{Y}(e)[Y(e)], con Es dataset, \hat{Y} il predittore e \hat{Y}(e)[Y(e)] è il valore della predizione \hat{Y}(e) valutato per l’Y(e) effettivo. Il logaritmo abbassa la complessità della funzione.

L’obiettivo di un buon predittore è quello di minimizzare la log loss o, in alternativa, massimizzare la likelihood, ovvero quanto verosimilmente il valore predetto è corretto rispetto al valore effettivo: \text{likelihood} = \displaystyle \prod_{e \in Es} \hat{Y}(e)[Y(e)]

\text{loglikelihood} = \displaystyle \sum_{e \in Es} \log \hat{Y}(e)[Y(e)] La log loss media è appropriata per predizioni nel ragionamento sotto incertezza. Ad esempio, sotto loss quadratica, 10^{-7} e 10^{-6} sono molto vicini, ma in termini di probabilità e log-loss, sono casi molto diversi, perchè vi è un ordine di grandezza di differenza.

3.3 Feature target booleane

Una variabile target booleana può essere trattata come una previsione a valore reale o come una previsione categorica. La predizione come valore reale è equivalente alla predizione categorica dove la predizione di 1 è p e quella per 0 è 1 - p.

Per l’errore, definiamo la log loss binaria: logloss(p, a) = - [a \log p + (1 - a) \log(1 -p)]con p predizione e a valore effettivo. La log-loss sarà log p quando a = 1, e log (1 - p) quando a = 0.

4 Stime puntuali senza feature di input

Il caso più semplice di apprendimento è quando vi è una sola feature di output e le feature di input sono ignorate. In questo caso, l’algoritmo predice uno stesso valore della feature target per tutti gli esempi. Questo forma una baseline naive che qualsiasi altro algoritmo dovrebbe riuscire a battere.

La predizione ottimale dipende dal criterio da ottimizzare.

Con Y numerica: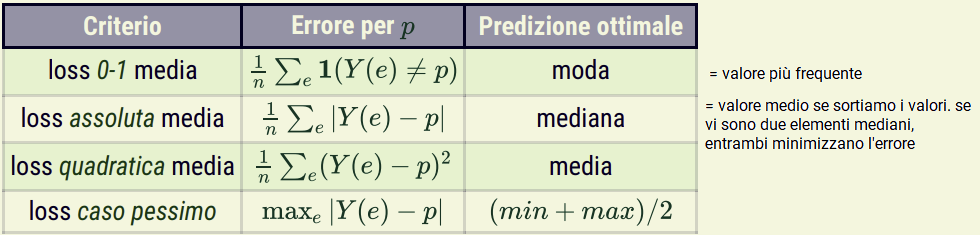

Con Y binaria: gli n esempi di training possono essere riassunti da n_1, cioè il numero di esempi con valore 1, ed n_0 = n - n_1. La media (e anche stima di massima verosimiglianza) è data dalla frequenza empirica, cioè dal numero di esempi con valore 1 sul totale degli esempi.

La moda minimizza la loss assoluta.

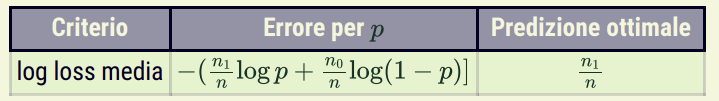
Con Y categorica con dominio {v_1, …, v_k}: il dataset può essere riassunto da k numeri n_1, …, n_k, dove n_i è il numero di occorrenze di v_i nel dataset. In questo caso la log-loss è minimizzata dalla predizione della frequenza empirica sul training set.

La moda minimizza l’errore 0-1 e massimizza l’accuratezza.

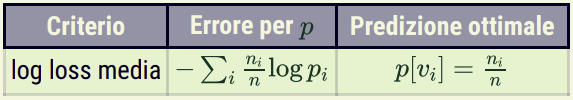
Pertanto, la scelta della predizione da preferire dipende dal modo in cui la predizione viene rappresentata e da come verrà valutata.

Questa analisi non specifica la previsione ottimale per gli esempi non visti. Non ci si deve aspettare che la frequenza empirica dei dati di addestramento sia la previsione ottimale per i nuovi esempi quando si massimizza la verosimiglianza o si minimizza il log loss. Se n_i = 0, allora v_i non appare nel training data, se però un solo esempio di test ha valore v_i, la likelihood è 0 e la log loss indefinita, si avrebbe quindi overfitting.

5 Tipi di errore

5.1 Misure per un modello predittivo binario

• Precision: \dfrac{tp}{tp + fp}

• Recall: \dfrac{tp}{tp + fn}

• False-positive rate (FPR): \dfrac{fp}{fp + tn}

5.2 Scelta del modello predittivo

L’ideale sarebbe massimizzare precision e recall e minimizzare la FPR, ma questo è utopia: all’aumentare della precision la recall diminuirebbe, cioè andremmo a fare predizioni positive solo se molto sicuri; di contro, massimizzando il richiamo si farebbero previsioni più azzardate, riducendo la precisione e aumentando l’FPR.

5.3 Costo

Supponiamo che i falsi positivi siano c volte peggiori dei falsi negativi:

• c < 1: falsi negativi peggiori dei falsi positivi

• c = 1: ugualmente pessimi

• c > 1: falsi positivi peggiori dei falsi negativi

Assumendo che il costo dell’errore venga aggiunto, il costo di una predizione è proporzionale a c \cdot fp + fn. Si dovrebbe scegliere il predittore con il costo più basso.

5.4 Spazio ROC e AUC

Il predittore A domina B se A ha recall maggiore e FPR minore di B, pertanto sarà migliore di B per tutte le funzioni che dipendono solo dal numero di falsi positivi e falsi negativi.

Per un dato insieme di esempi dove sia la predizione che il valore attuale è dato, lo spazio ROC è un grafico che plotta il FPR contro la recall per vari predittori, ognuno di questi produce un punto nello spazio.

Per alcuni modelli vi sono degli iperparametri che, variati, portano a diversi FPR e recall. In questi casi si avrebbe una curva nello spazio ROC al variare del parametro, ed un algoritmo è migliore dell’altro se la sua curva è al di sopra e più a sinistra. Spesso due algoritmi si dominano a vicenda in diversi punti, pertanto si ricorre all’area sotto la curva ROC (AUC), ovvero una misura numerica per confrontare il modello nello spazio degli iperparametri, sotto una particolare funzione di costo.

6 Modelli base

6.1 Alberi di decisione

Un albero di decisione è un albero in cui:

• Ogni nodo interno è etichettato con una condizione

• Ogni nodo interno ha due figli, gli archi da padre a figlio sono etichettati con true e false

• I nodi foglia sono etichettati con una stima puntuale della classe (classificazione) o con una stima puntuale di un valore reale (regressione)

Per classificare un esempio l’albero agisce in questo modo: partendo dalla radice, ogni condizione incontrata viene valutata e si segue l’arco corrispondente al risultato, raggiunta una foglia si restituisce la relativa stima puntuale.

Vi sono due questioni da considerare:

• Quale albero generare? Poichè un albero di decisione può rappresentare qualsiasi funzione con delle feature di input discrete, il bias è incorporato nella preferenza di un albero rispetto che all’altro. Un’idea è quella di preferire gli alberi meno profondi, o con meno nodi, comunque coerenti con i dati (rasoio di Occam: definizioni più corte della funzione sono quelle che massimizzano la likelihood).

• Come generare l’albero? Lo spazio di ricerca è enorme, pertanto si effettua una ricerca greedy dove si parte da alberi piccoli, per poi complicarli se non soddisfano certe condizioni, con goal di minimizzare l’errore.

6.1.1 Ricerca di buoni alberi di decisione

L’algoritmo effettua una scelta miope della condizione c ottimale, perchè sceglie una condizione alla volta che magari è buona per quel passo per dividere lo spazio di ricerca, ma i sottoalberi potrebbero poi risultare complicati da sfruttare, scartando magari condizioni subottimali che “spaccano” meglio lo spazio di ricerca più in profondità. In sostanza l’algoritmo non garantisce di restituire l’albero ottimo globale.

La scelta della condizione usata è chiamata greedy optimal split ed è basata sulla somma delle loss prima e dopo il partizionamento, che viene confrontata con il valore ottenuto dalla somma delle loss degli esempi scalati per un fattore \gamma, in modo da penalizzare l’albero nel momento in cui le dimensioni aumentano.

Il criterio di stop si “attiva” quando le condizioni sono esaurite o se si hanno solo esempi di una stessa classe, e quindi ho loss nulla. In alternativa altri criteri per stop anticipati sono il minimum child size (figlio con meno esempi rispetto a una data soglia) e la maximum depth (profondità massima raggiunta)

Quando la loss usata è la log loss con base 2, la media delle loss \dfrac{\text{sum\_losses}(es)}{|Es|} è l’entropia della distribuzione empirica di Es. Il numero di bit necessari per descrivere Es dopo aver testato la condizione è val, l’entropia della distribuzione creata dallo split è \dfrac{val}{|Es|}. La differenza tra i due è l’information gain dello split, alcune volte utilizzato come euristica anche quando il criterio di ottimalità è un’altra misura di errore.

6.1.2 Feature di input non Booleane per alberi di decisione

• X categorica

  • Si associa una variabile indicatrice binaria X_i a ciascun valore, dove X_i(e) = 1 se X(e) = v_i, X_i(e) = 0 altrimenti. Per ogni esempio e una sola fra X_i(e) vale 1, le altre sono nulle.

• X ordinale (dominio totalmente ordinato): comprende feature continue o discrete.

  • Per ciascun valore v, una feature Booleana può essere costruita come un taglio: una nuova feature che ha valore 1 quando X > v, 0 altrimenti. Combinando vari tagli si possono creare degli intervalli per cui la feature è vera o falsa. I valori ottimali di cut vengono trovati con tecnica trial and error, cioè ordinando gli esempi in base al valore di X e selezionare i tagli che partizionano meglio lo spazio di ricerca.

  • In alternativa si può usare il binning, ovvero dato un insieme di soglie, si crea una feature per ogni intervallo. Le soglie a_1 < a_2 < … < a_k creano k + 1 feature Booleane, di cui una è vera per X quando X \leq a_1, una vera quando a_k < X, e una vera per a_i < X \leq a_{i+1} per ogni 1 \leq i < k. Prevedo quindi sempre 2 figli ma usando 2 limiti, testo l’appartenenza su più vincoli.

• E’ possibile espandere l’algoritmo su condizioni n-arie, prevedendo un albero n-ario, dove ogni figlio è un valore del dominio, trasformando un albero if-then-else in albero switch. Questo approccio è problematico per motivi di gain ratio: per euristiche greedy come l’information gain, è meglio splittare su una variabile con un dominio più largo perchè produce più figli e quindi può adattarsi meglio ai dati, anche se splittare su feature con piccoli domini mantiene la rappresentazione più compatta.

6.2 Regressione e Classificazione Lineare

La regressione lineare è il problema di adattare una funzione lineare, ovvero uno schema prefissato in cui cambiano solo i parametri, a un training set con feature di input e target numeriche. Date le feature di input X_1, …, X_m \in \mathbb{R} e target: Y \in \mathbb{R}, una funzione lineare delle feature di input ha la forma: \hat{Y}_{W}(e) = w_0 \cdot X_0(e) + w_1 \cdot X_1(E) + ... + w_m \cdot X_m (e) = \displaystyle \sum_{i = 0}^m w_i \cdot X_i (e)

dove W è il vettore di pesi e X_0 è una feature costante il cui valore è sempre 1.

Possiamo vedere la regressione lineare come un problema di ottimizzazione: dato l’insieme di esempi E, l’errore quadratico medio su E per Y è: error(E,W) = \displaystyle \dfrac{1}{|E|} \sum_{e \in E} (\hat{Y}_{W} (e) - Y(e))^2 = \dfrac{1}{|E|} \sum_{e \in E} \left(\sum_{i = 0}^m w_i \cdot X_i(e) - Y(e)\right)^2 La formula ha un unico minimo che occorre quando le derivate parziali rispetto ai pesi sono nulle: \dfrac{\partial}{\partial w_i} = \dfrac{1}{|E|} \displaystyle \sum_{e \in E} 2 \partial(e) \cdot X_i (e) con X_i(e) costante e \partial (e) = \hat{Y}_{W}(e) - Y(e) è una funzione lineare sui pesi.

I pesi che minimizzano l’errore possono essere calcolati analiticamente ponendo la derivata parziale a 0 e risolvendo le equazioni lineari nei pesi. Un predittore basato su tale funzione è detto classificatore lineare.

Ora consideriamo una classificazione binaria. Una funzione lineare non funziona bene perchè le predizioni non saranno necessariamente comprese tra 0 e 1, pertanto serve una funzione che, applicata sulla funzione lineare, dia k valori e delle predizioni comprese tra 0 e 1.

Una funzione lineare compressa è della forma: \hat{Y}_W (e) = \phi (w_0 \cdot X_0 + w_1 \cdot X_1(e) + ... + w_m \cdot X_m(e)) = \phi \left(\displaystyle \sum_i w_i \cdot X_i(e)\right)

\phi è detta funzione di attivazione, ed è la funzione che permette di portare la funzione lineare da [-\infty, \infty] a [0, 1].

La funzione di attivazione più semplice è la funzione scalino: step(x) = \begin{cases} 0 \;\;\; x < 0 \\ 1 \;\;\; x \geq 0 \end{cases}

Questa funzione di attivazione è alla base del percettrone, ma è difficile adattare la discesa del gradiente a funzioni non ovunque differenziabili, pertanto non abbiamo convergenza garantita, l’ampiezza dello scalino dovrebbe tendere a 0.

Una funzione di attivazione ovunque differenziabile è la funzione sigmoide o funzione logistica: sigmoid(x) = \dfrac{1}{1 + e^{-x}} la cui derivata è: \dfrac{d}{dx} sigmoid(x) = sigmoid(x) \cdot (1 - sigmoid(x))

6.3 Regressione logistica

La regressione logistica è un modello di classificazione basato su una funzione lineare appiattita dal sigmoide: \hat{Y}(e) = sigmoid \left( \displaystyle \sum_{i = 0}^m w_i \cdot X_i (e)\right)

Per trovare i pesi si minimizza la log-loss media: LL(E, W) = - \dfrac{1}{|E|} \left[ \displaystyle \sum_{e \in E} Y(e) \log \hat{Y}(e) + (1 - Y(e)) \log (1 - \hat{Y}(e))\right]

con derivate parziali:

\dfrac{\partial}{\partial w_i} LL (E, W) = \dfrac{1}{|E|} \displaystyle \sum_{e \in E} \partial(e) \cdot X_i (e) con \partial(e) = \hat{Y}_W(e) - Y(e).

Essendo una funzione esponenziale applicata su funzione lineare trovare gli zeri è più difficile, pertanto è difficile da minimizzare analiticamente.

6.3.1 Discesa di gradiente

Il problema di trovare un set di parametri che minimizzano gli errori è un problema di ottimizzazione, risolvibile con la discesa di gradiente: si scelgono casualmente i valori di W e si decrementa ogni peso w_i in proporzione alla relativa derivata parziale:

w_i = w_i - \eta \cdot \dfrac{\partial}{\partial w_i} error(E, W)con \eta learning rate, riducibile ad esempio in funzione del tempo. Le derivate parziali misurano l’influenza sull’errore di piccole variazioni dei pesi.

Un’implementazione diretta della discesa di gradiente non aggiorna alcun peso fin quando tutti gli esempi non sono stati considerati, e questo può risultare pesante per dataset grandi.

6.3.2 Discesa di gradiente stocastica

E’ possibile fare progressi con un sottoinsieme dei dati casuale, aggiornando i pesi quindi non dopo aver visto tutti gli esempi.

Il set di b esempi usati in ogni update chiamato batch. Un passaggio completo su tutto il dataset è detto epoca, ed è formato da \dfrac{|E|}{b} batch, in modo da convergere. L’algoritmo termina dopo un certo numero di passi, se l’errore è molto vicino allo 0, o se le oscillazioni di W sono tali da poter considerare i pesi stabili.

I batch più piccoli tendono ad apprendere più velocemente, poiché sono necessari meno esempi per un aggiornamento. Tuttavia, potrebbero non convergere verso un ottimo locale. Utilizzando un batch contenente tutti gli esempi di addestramento, tutte le derivate sarebbero zero: non è necessario apportare alcuna correzione ai pesi se si è già in una posizione ottimale. Con batch più piccoli, i pesi del modello varieranno di più, e i batch successivi potrebbero utilizzare impostazioni di parametri non ottimali. Questo può rendere difficile la convergenza. È consuetudine iniziare con un batch di piccole dimensioni e aumentarlo fino a quando non si ottiene la convergenza o prestazioni soddisfacenti.

6.4 Separabilità lineare

Ogni feature può essere vista come una dimensione: m feature formano uno spazio m-dimensionale.

Un iperpiano è un sottospazio che ha una dimensione in meno rispetto allo spazio ambiente e può essere utilizzato per dividere lo spazio in due metà, in alternativa può essere visto come un insieme di punti che soddisfano un vincolo espresso come equazione lineare sulle variabili. In uno spazio m-dimensionale determina uno spazio con (m - 1) dimensioni.

Un problema di classificazione booleano è linearmente separabile se esiste un iperpiano che separi gli esempi delle due classi.

Una classificazione binaria linearmente separabile è apprendibile con la regressione logistica o con la discesa di gradiente stocastica, e l’iperpiano è l’insieme dei punti \displaystyle \sum w_i \cdot X_i = 0 dove w_i sono i pesi appresi.

Da un lato dell’iperpiano, la predizione sarà maggiore di 0.5, dall’altra minore di 0.5.

6.5 Feature target categoriche

Quando il dominio di target è categorica (con più di 2 valori), l’idea è quella di apprendere una funzione lineare per ogni valore di target, fare l’esponenziale, e normalizzare. Questo porta ad avere più parametri, ma tratta tutti i valori allo stesso modo. Questa funzione si chiama softmax: prende un vettore di numeri reali (a, …, a) e restituisce un vettore della stessa dimensione dove l’i-esima componente del risultato è:

softmax((a_1, ..., a_k))_i = \dfrac{exp(a_i)}{\displaystyle \sum_{j = 1}^k exp(a_j)}

Questo assicura che i valori siano positivi e sommino a uno, potendo quindi considerare il vettore risultante come una distribuzione di probabilità.

Una softmax((0, x))_2 è uguale a una sigmoide(x), dove (0, x) corrispondono ai valori (false, true).

Una softmax, come la sigmoide, non può rappresentare probabilità nulle.

Una generalizzazione della regressione logistica è chiamata regressione softmax (o regressione logistica multinomiale). Questa coinvolge un’equazione lineare per ogni valore nel dominio della feature target. Supponiamo Y = (v_i, …, v_k), la predizione per l’esempio e è una tupla di k valori softmax((u_1(e), …, u_k(e))), dove il j-esimo componente è la predizione Y = v_j e:

u_j(e) = w_{0 , j} + X_1 (e) \cdot w_{1 ,j} \cdot + ... + X_m(e) \cdot w_{m, j}

Questa è ottimizzata usando la log loss categorica:

\dfrac{\partial}{\partial w_{ij}} logloss(softmax(u_1(e), ..., u_k(e)), v_q) = (\hat{Y}(e)_j - 1(j = q)) \cdot X_i dove 1(j = q) è 1 se j è l’indice del valore osservato v_q e \hat{Y}(e)_j è la j-esima componente della predizione. Questo è il valore predetto meno quello effettivo.

Per implementare in maniera efficiente questo si può aggiungere una costante a ogni a_i che non altera il valore ed evita problemi di overflow e underflow.

6.6 Creazione di feature di input

La definizione di regressione lineare e logistica assumono che le feature di input siano numeriche.

Feature categoriche possono essere convertite in feature con dominio {0, 1} usando variabili indicatrici. Questo è detto one-hot encoding.

Feature reali possono essere usate direttamente se il target è una funzione lineare di questa feature di input, una volta aggiustate le altre feature di input. Se il target non è una funzione lineare, possono essere usate altre trasformazioni.

Per feature ordinali, comprese quelle a valori reali, definiamo dei tagli per definire variabili booleane: la feature di input x è vera se scelto un valore v risulta che x < v, falsa altrimenti.

In alternativa si fa feature engineering, ovvero l’ingegnerizzazione di nuove feature sulla base di quelle già esistenti.

7 Overfitting

L’overfitting avviene quando i modelli fanno delle predizioni basandosi su regolarità che appaiono nei dati di esempio, ma non nel mondo reale. Questo succede quando il modello tenta di trovare dei segnali in una distribuzione casuale di dati, quindi correlazioni che non si riflettono poi sull’intero dominio del problema, o quando il predittore diventa troppo confidente.

Questo fenomeno è legato alla regressione verso la media, ovvero che i valori sono determinati da qualità e caso, più dati si ha a disposizione e più si abbassa l’impatto della casualità. L’overfitting può essere causata anche dalla complessità del modello: un modello più complesso, con più parametri, ha più facilità di adattarsi troppo ai dati di training.

7.1 Errore sul test set

L’errore sul test set è causato da bias, varianza e rumore:

• Bias: errore dovuto all’imperfezione del modello appreso. Il bias è basso quando il modello è vicino alla vera “funzione” dietro ai dati (ground truth). Il bias è decomponibile in bias di rappresentazione, causato dalla mancanza di un’ipotesi vicina alla ground truth, e bias di ricerca, causato da un algoritmo che non cerca esaustivamente lo spazio di ipotesi.

  • Un albero di decisione ha bias di rappresentazione basso (si può rappresentare qualunque funzione) ma bias di ricerca crescente con il numero di feature (moltissimi alberi)

  • Una regressione lineare ha bias di rappresentazione alto ma bias di ricerca nullo se risolta analiticamente. Se si usa la discesa di gradiente invece il bias di ricerca è maggiore.

• Varianza: errore dovuto alla limitatezza dei dati disponibili. Un modello complesso, con tanti parametri, richiede tanti dati. Con un quantitativo di dati fisso vi è un compromesso tra bias e varianza, si può avere un modello complesso con bias basso e alta varianza perchè il quantitativo di dati necessario per fare una stima puntuale non è disponibile, o un modello semplice non molto accurato, ma che può stimare i parametri abbastanza bene, quindi bassa varianza e bias alto.

• Rumore: errore dovuto a dati che dipendono da feature non considerate nel modello o perchè il processo di generazione dei dati è inerentemente stocastico.

L’errore sul training set diminuisce con l’aumentare del numero di iterazioni. Per l’insieme di test, l’errore raggiunge un minimo e poi aumenta con l’aumentare del numero di iterazioni. Man mano che si adatta agli esempi di addestramento, gli errori nell’insieme di test diventano più grandi, perché il modello imperfetto diventa più sicuro.

7.2 Rimedi all’overfitting

7.2.1 Pseudoconteggi

Spesso la media è una predizione ottimale rispetto a molte altre misure di predizione. In caso di dati booleani, la media può essere interpretata come probabilità. La media empirica del training set non è però un buon predittore della probabilità di nuovi casi, poichè un valore non osservato avrebbe probabilità nulla. Per risolvere questo problema della probabilità nulla si utilizza della conoscenza pregressa per creare degli pseudoesempi che verranno aggiunti agli esempi in nostro possesso.

Quindi, disponendo dei valori osservati v_1, …, v_n, si vuole predire \hat{v}. Se n = 0, si assuma di usare una predizione a_0 che non può essere basata sui dati, perchè non ne esistono. In altri casi: \hat{v} = \dfrac{c \cdot a_0 + \sum_i v_i}{c + n} dove c è il numero di pseudoesempi con valore a_0 (media mobile). c può essere un qualsiasi numero reale non negativo, se c = 0 la predizione è la media, ma questa non può essere usata con n = 0.

Il valore di c regola l’importanza fra ipotesi iniziale (a priori) e dati.

7.2.2 Regolarizzazione

Il Rasoio di Occam ci dice che è meglio preferire modelli semplici a quelli complessi. Seguendo questa intuizione, l’idea è quella di introdurre un regolarizzatore, ovvero un termine da aggiungere alla misura di errore in modo da penalizzare la complessità dell’ipotesi da apprendere.

La tipica forma di un regolarizzatore è quella di trovare un predittore \hat{Y} che minimizzi \left( \displaystyle \sum loss(\hat{Y}(e), Y(e))\right) + \lambda \cdot regularizer(\hat{Y}), dove la loss misura la qualità dell’adattamento all’esempio e, e regularizer(\hat{Y}) è il termine di penalità per la complessità. Il parametro di regolarizzazione, λ, rappresenta un compromesso tra l’adattamento ai dati e la semplicità del modello. All’aumentare del numero di esempi, la somma più a sinistra tende a dominare e il regolarizzatore ha un effetto limitato. Il regolarizzatore ha un effetto maggiore quando gli esempi sono pochi. Il parametro di regolarizzazione è necessario perché i termini di errore e complessità sono tipicamente in unità diverse.

Il regolarizzatore è un iperparametro, cioè un parametro usato per definire cosa va ottimizzato. Questo può essere ottenuto da esperienze pregresse o con CV.

Negli alberi di decisione la complessità può essere misurata sul numero di foglie, che è 1 + numero di split per un albero binario. Quando si costruisce un albero di decisione, si può ottimizzare l’errore minimizzando: \sum_{e \in E} loss(\hat{Y}(e), Y(e)) + \gamma \cdot |foglie|Un singolo split su una foglia aumenta il numero di foglie di 1, pertanto lo split avrà senso se questo riduce l’errore di \gamma.

Per modelli con parametri a valori reali, si usa un regolarizzatore L_2, ovvero un regolarizzatore della somma dei quadrati dei pesi (norma 2): |w|_2^2 = w_1^2 + w_2^2 + ... + w^2_n, pertanto pesi vicino allo 0 hanno poco peso, mentre pesi “outlier” possono avere un grosso impatto. Quando si ottimizza l’errore quadratico per la regressione logistica con un regolarizzatore L_2 si parla di ridge regression, ed è equivalente ad avere \lambda pseudoesempi con valore 0 per la feature target, e 1 per tutte le feature di input.

Un regolarizzatore L_1 aggiunge una penalità alla somma dei valori assoluti dei parametri. Quando si ottimizza l’errore quadratico per la regressione logistica col regolarizzatore L_1 si parla di LASSO.

Il regolarizzatore L_2 penalizza w^2, il regolarizzatore L_1 penalizza |w|, quindi hanno derivate differenti, il regolarizzatore L_2 ha derivata 2 \cdot w, mentre L_1 ha derivata k costante indipendente dal peso. L_2 quindi normalmente non guida i pesi verso l’annullamento, mentre la derivata di L_1 può essere pensata come una forza che sottrae una certa costante dal peso ogni volta. Questo significa che L_1 tende ad annullare molti pesi, facendo ignorare le relative feature. In sostanza si può fare feature selection sfruttando il regolarizzatore L_1.

7.2.3 Cross Validation

L’idea della cross validation è quella di trattenere parte dei dati di training per valutare un modello appreso sulla base del resto degli esempi di training. Si dividono i dati non di test in due parti:

• insieme di training su cui allenare i modelli

• insieme di validazione per valutare i modelli, ovvero per individuare la miglior configurazione degli iperparametri (la lista la fornisco io se uso un’implementazione basata su GridSearch)

  • l’insieme di validazione non viene usato per la scelta degli iperparametri

La CV si ripete scambiando i ruoli degli esempi per ottenere modelli diversi. In genere, si vuole addestrare il maggior numero possibile di esempi, per ottenere modelli migliori. Tuttavia, un set di addestramento più grande si traduce in un set di validazione più piccolo, e un set di validazione piccolo può o meno adattarsi bene solo per fortuna (casualità). Tipicamente l’addestramento ha bisogno di molti esempi per avere modelli migliori, ma ciò non deve andare a scapito del validation set.

Con pochi dati, si usa la k-fold cross validation, ovvero gli esempi vengono utilizzati sia per il training che per la validazione per regolare i parametri (quindi la complessità) del modello appreso. Si partiziona casualmente il dataset in k parti di uguali dimensioni (fold) e si addestra il modello k volte, ognuna con una distinta fold per la validazione. La validazione coinvolgerà ogni esempio in una fold. A questo punto si determinano e si restituiscono gli iperparametri con le impostazioni ottimali, allenati su tutti i dati.

Quando k è pari al numero di esempi di training si parla di leave one out cross validation. Con n esempi nel training set, si apprendono n modelli, per ogni esempio e si utilizzano tutti gli altri esempi per addestrare un modello, e si valuta il modello su e. E’ la forma statisticamente più robusta, ma anche la più pesante computazionalmente. Questo non è pratico se il training è fatto indipendentemente, perchè all’aumentare del numero di esempi la complessità aumenterebbe. Si potrebbe utilizzare se il modello creato in una esecuzione può essere modificato in modo efficiente nel successivo, sostituendo un solo esempio con un altro.

8 Estensione dei modelli lineari

L’idea per risolvere problemi non linearmente separabili è quella di cambiare la rappresentazione dei dati con nuove feature, che aumentano la dimensionalità dello spazio.

8.1 Funzione kernel

Una funzione kernel è una funzione che viene applicata sulle feature di input per creare nuove feature. Aggiungendo queste nuove feature si possono creare dei separatori lineari dove prima non ce n’erano. Ad esempio, per una feature x, aggiungere x^2 e x^3 alle feature permette di definire un linear learner per trovare il miglior polinomio di terzo grado. Quando lo spazio delle feature viene aumentato, l’overfitting può diventare un problema. Le funzioni kernel sono spesso ristrette a casi in cui l’addestramento su spazi aumentati può essere implementato in maniera efficiente.

8.2 Reti neurali

Le reti neurali ammettono input alla funzione lineare appiattita che sono a loro volta funzioni lineari appiattite con dei pesi da determinare. Avere più layer di funzioni lineari appiattite come input a funzioni lineari appiattite permette di rappresentare funzioni più complesse

8.3 Alberi di regressione

I regression tree sono alberi di decisione dove le foglie hanno delle funzioni costanti, che rappresentano una funzione lineare per parti. E’ possibile avere delle reti neurali o altri classificatori alle foglie degli alberi di decisione. Per classificare un nuovo esempio, l’esempio viene instradato giù per l’albero dalla radice a una foglia e si usa il modello contenuto nella foglia per classificarlo.

9 Ensemble Learning

Nell’ensemble learning si combinano le predizioni di weak learner, ovvero modelli apparentemente deboli che messi insieme diventano un modello che si comporta bene.

Un semplice ma efficace modello composito è il random forest, dove si utilizzano tanti alberi di decisione, ognuno dei quali può creare una predizione per ogni esempio.

Per rendere questo efficiente, ogni albero deve fare diverse predizioni. Per assicurare la diversità delle predizioni si possono usare le seguenti tecniche:

• Ogni albero utilizza un sottoinsieme diverso di esempi per essere allenato. Nel bagging, il sottoinsieme randomico è selezionato per ogni albero. In ogni sottoinsieme, alcuni esempi non vengono scelti e altri sono duplicati.

• Si sceglie un insieme ristretto di feature da considerare per uno split.

Una volta che gli alberi sono stati addestrati, le predizioni degli alberi vengono combinate (majority voting), usando un metodo appropriato come criterio di ottimalità, come ad esempio la moda delle predizioni dell’albero per massimizzare l’accuratezza, oppure la media delle predizioni dell’albero se il problema è di regressione, per minimizzare l’errore quadratico.

9.1 Boosting

Nel boosting viene usata una sequenza di modelli costruiti imparando dagli errori dei precedenti. Le caratteristiche di un algoritmo di boosting sono le seguenti:

• C’è una sequenza di base learners uguale o differente. Questi possono anche essere weak learner, quindi modelli deboli e non necessariamente ottimali, che devono giusto superare un classificatore casuale.

• Ogni learner viene allenato per adattarsi agli esempi a cui il precedente learner non si è adattato bene

• La predizione finale è ottenuta aggregando le predizioni dei modelli prodotti

Fra gli algoritmi più noti di questo tipo c’è ADABoost.

Un semplice algoritmo di boosting è il functional gradient boosting, usato per la regressione come segue: l’algoritmo ha K iperparametri, che è il numero di modelli base da utilizzare. La predizione finale sarà data in funzione degli input come:

p_0 + d_1(X) + ... + d_K(X) dove p_0 è la predizione iniziale, e ogni d_i è la differenza dalla predizione precedente. L’i-esima predizione è infatti:

p_i(X) = p_0 + d_1(X) + ... + d_i(X) = p_{i - 1}(X) + d_i(X)

Ogni d_i è costruito dal weak learner minimizzando l’errore di p_i, dato p_{i -1}. Ad ogni passo, il base learner impara a minimizza \hat{d_i}:

\sum loss(p_{i-1}(e) + \hat{d_i}(e), Y(e)) = \sum loss(\hat{d_i}(e), Y(e) - p_{i - 1}(e))

per una qualsiasi loss basata sulla differenza tra valore attuale e valore predetto (no log loss).

L’i-esimo learner impara d_i(e) ad adattarsi su Y_i(e) - p_{i - 1}(e). Questo è equivalente ad allenare su un dataset modificato, dove le predizioni precedenti vengono sottratte dal valore attuale nel training set. In questo modo ogni learner è costruito in modo da correggere gli errori della predizione precedente.