8. Learning with Uncertainty
Dato il dataset E, il teorema di Bayes specifica come determinare la probabilità di un modello m dato E: P(\text{m | E}) = \dfrac{P(\text{E | m}) \cdot P(m)}{P(E)}
P(E | m) è la verosimiglianza che E sia stato generato da m. E’ alta quando il modello è una buona approssimazione della distribuzione dei dati
P(m) è la probabilità a priori e codifica il learning bias, ovvero la propensione a sbilanciarsi verso un modello rispetto che un altro indicando i modelli più verosimili a priori e può essere usata per indurre a scegliere modelli più semplici attribuendogli una maggiore probabilità a priori: se vado verso modelli più semplici diminuisco il bias sull’errore
P(E) è la funzione di partizione ed è una costante di normalizzazione, in modo che le probabilità sommino a 1, avendo quindi una distribuzione di probabilità
L’obiettivo è quello di trovare il modello che meglio si adatta ai dati.
Possiamo scegliere un modello ML (modello di massima verosimiglianza), ovvero un modello che massimizza P(E | m), dando quindi lo stesso peso (P(m)) ad ogni modello. Il problema è che se lo spazio dei modelli è molto ricco, è molto probabile che ci siano tanti modelli che si adattano bene (P(E | m) = 1), portando a overfitting, mentre magari un modello molto poco probabile a priori potrebbe essere quello corretto e risultare anche il migliore.
Possiamo anche scegliere un modello che massimizza P(m | E) detto modello MAP (Maximum a posteriori probability model), ovvero un modello che massimizza il numeratore (il denominatore è indipendente dal modello e può essere ignorato): P(\text{E | m}) \cdot P(m)
E’ basato sulla likelihood (adattamento ai dati) e distribuzione a priori dei modelli, che può essere usato come learning bias tenendo sotto controllo la complessità del modello.
Se P(m) è uniforme, i due modelli sono uguali, se non è uniforme bisogna preferire modelli più semplici, meno soggetti a overfitting, seguendo il rasoio di Occam.
1 Apprendimento bayesiano
L’apprendimento bayesiano consiste nello scegliere in base alla probabilità a posteriori dei modelli dati gli esempi, invece di scegliere il singolo modello più verosimile: P(Y\text{ | }X = x \land E)
Y è la feature target
X = x sono le feature di input del singolo esempio di test
Il ruolo di un modello è quello di essere il generatore presunto degli esempi. L’idea di questo approccio è quella di lavorare con tutti i modelli cercando di sfruttare le distribuzioni di probabilità di ogni modello.
Dato un insieme M di modelli disgiunti, si determina:
\begin{aligned} P(Y | X = x \land E) & = \sum_{m \in M} P(Y \land m | X = x \land E) && (1) \\ & = \sum_{m \in M} P(Y | m \land X = x \land E) \cdot P(m | X = x \land E) && (2) \\ & = \sum_{m \in M} P(Y | m \land X = x) \cdot P(m | E) && (3) \end{aligned}
Introduco m rispetto a y considerando tutti i modelli che posso costruire
Il modello include tutte le informazioni su E necessarie a una predizione
Il modello non cambia rispetto a un nuovo esempio.
P(m | E) lo calcolo con Bayes.
Invece di prendere il modello migliore l’apprendimento bayesiano si basa sul model averaging, ovvero la media delle predizioni di tutti i modelli pesati sulla probabilità a posteriori dati gli esempi di training.
Rispetto a un modello MAP è più preciso perchè con un modello MAP ne scelgo uno, qui li utilizzo tutti e cerco di prendere il meglio da tutti i modelli.
Tipicamente si assume che gli esempi sono indipendenti e identicamente distribuiti: P(E | m) = \displaystyle \prod_{i = 1}^k P(e_i | m) rappresentabile come belief network:
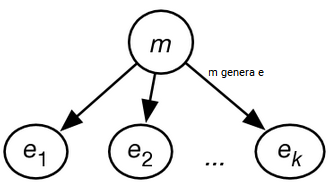
Una tecnica di ragionamento in una rete di questo tipo consiste nel condizionare gli e_i osservati e nell’interrogare una variabile e_j non osservata, che fornisce una previsione probabilistica per gli esempi non visti, oppure nell’interrogare m, che fornisce una distribuzione sui modelli.
1.1 Apprendere probabilità
1.1.1 Variabile booleana
Il caso più semplice è quello di imparare un singolo booleano senza feature in input, l’obiettivo è quello di imparare la distribuzione a posteriori di Y condizionata dagli esempi di training.
L’approccio bayesiano prevedere di trattare i parametri come variabili aleatorie a valori reali, dove se i valori tendono a infinito le sommatorie vanno viste sotto integrali.
Per Y booleana, una variabile a valore reale \phi nell’intervallo [0, 1] rappresenta la probabilità di Y: P(Y = true | \phi) = \phi e P(Y = false | \phi) = 1 - \phi.
Supponiamo che per P(\phi) inizialmente un agente consideri tutti i valori nell’intervallo [0,1] con la stessa probabilità di essere il valore di ϕ. Questo può essere modellato con la variabile ϕ che ha una distribuzione uniforme sull’intervallo [0, 1]. Questa è la funzione di densità di probabilità etichettata n_0 = 0, n_1 = 0.
La distribuzione di probabilità di \phi viene poi aggiornata condizionando sugli esempi osservati. Gli esempi in E saranno una sequenza di osservazioni con un numero di occorrenze n_1 di Y = true e n_0 occorrenze di Y = false: P(\phi | E) = \dfrac{P(E | \phi) \cdot P(\phi)}{P(E)} \propto^{i.i.d.} \phi^{n_1} \cdot (1 - \phi)^{n_0} \cdot P(\phi)
La distribuzione di questo esempio è la distribuzione Beta: Beta_{\alpha_0, \alpha_1} (\phi) = \dfrac{1}{Z} \phi^{\alpha_1 - 1} \cdot (1 - \phi)^{\alpha_0 - 1}
\phi^{\alpha_1 - 1} sono i casi veri a priori
(1 - \phi)^{\alpha_0 - 1} sono i casi falsi a priori
Z è una costante di normalizzazione, che ci assicura che l’integrale sia 1
moda (valore con max probabilità): \phi = \dfrac{\alpha_1 - 1}{\alpha_0 + \alpha_1 - 2}
valore atteso: \phi = \dfrac{\alpha_1}{\alpha_0 + \alpha_1}
Queste probabilità ce le dice ad esempio l’esperto.
La distribuzione a priori non deve essere necessariamente uniforme, ma si possono usare degli pseudo-esempi, quando non ho esempi mi sbilancio verso gli pseudo-esempi. Appena avremo nel tempo esempi mi sbilancio verso questi. In questo modo evito overfitting perchè non ho probabilità nulle in nessun momento.
Con gli pseudo-esempi:
P(\phi) = \phi^{c_1 - 1} \cdot (1 - \phi)^{c_0 - 1}
c_1 pseudo-esempi con Y = true, c_0 pseudo-esempi con Y = false
stima MAP per \phi: p = \dfrac{c_1 + n_1 - 1}{c_0 + n_0 + c_1 + n_1 - 2}
valore atteso: p = \dfrac{c_1 + n_1}{c_0 + n_0 + c_1 + n_1}
Se si hanno solo n_0 e n_1, che possono corrispondere a sequenze diverse di esempi, si ricorre a una distribuzione binomiale, dato che dobbiamo tenere in considerazione tutte le possibili sequenze che possono dare questo conto.
1.1.2 Variabile categorica
Sia Y una variabile categorica con k possibili valori. Una distribuzione su una variabile categorica è detta distribuzione multinomiale. La distribuzione Dirichlet è l’estensione della distribuzione Beta a più dimensioni:
Dirichlet_{\alpha_1 ,..., \alpha_k} (p_1, ..., p_k) = \dfrac{1}{Z} \displaystyle \prod_{j = 1}^k p_j^{\alpha_j - 1}
p_1, …, p_k sono i singoli valori che può assumere Y
\alpha_j \geq 0 sono i conteggi iniziali, p_j è la probabilità del j-esimo valore, Z è la costante di normalizzazione
il valore atteso per il risultato i-esimo mediando su tutti i p_j è \dfrac{\alpha_i}{\displaystyle \sum_j \alpha_j}
Per predire un valore per Y si parte dagli pseudo-conteggi positivi c_i per ogni y_i ottenuti prima di osservare dati. Si supponga poi che l’agente osservi n_j esempi con Y = y_j: la probabilità di Y è stimata usato il valore atteso
P(Y = y_j) = \dfrac{c_j + n_j}{\sum_h c_h + n_h}
Quando il dataset è vuoto (tutti n_i = 0) i c_i sono usati per stimare le probabilità. L’agente non deve partire obbligatoriamente da una distribuzione a priori uniforme, ma una qualsiasi. Se l’agente parte da una Dirichlet anche quella a posteriori sarà una Dirichlet.
Opinioni degli esperti
L’uso degli pseudo-conteggi permette di combinare la conoscenza degli esperti con i dati. L’idea è quella di chiedere per un dato P(A) all’esperto di fornire n occorrenze di A su m prove, cioè invece di provvedere con una probabilità, l’esperto da una stima delle dimensioni dei dati su cui fonda il parere.
I conteggi dei vari esperti vanno combinati per ricavare gli pseudo-conteggi. La proporzione dei conteggi riflette la probabilità, mentre i livelli di confidenza si riflettono nei valori assoluti: rappresentare P = \dfrac{2}{3} con n = 2 e m = 3 indica una bassa confidenza facilmente soppiantata da dati o stime di altri esperti, mentre n = 2000 e m = 3000 indica un’alta confidenza la cui influenza verrebbe ridotta solo da milioni di dati.
1.2 Classificatori probabilistici
Un classificatore di Bayes è un modello probabilistico di classificazione, dove la distribuzione a posteriori è calcolata con il teorema di Bayes.
L’idea è che la classe influenza i valori delle feature per le sue istanze (al contrario rispetto a un normale classificatore). Il fatto di appartenere alla stessa classe implica valori simili nelle feature, quindi gli esempi possono essere raggruppati in questo modo in classi. Imparando queste dipendenze delle feature dalla classe, si userà il modello risultane per predire la classificazione di nuove istanze.
1.2.1 Naive Bayes
Il caso più semplice è il classificatore Naive Bayes, che considera le feature di input X_i data Y indipendenti tra loro. L’indipendenza del classificatore Naive Bayes si concretizza in una belief network in cui le feature sono i nodi, la feature target (la classe) non ha genitori e la feature target è l’unico genitore di ogni feature di input. Questa belief network richiede le distribuzioni di probabilità P(Y) per Y e P(X_i | Y) per ogni X_i. La predizione viene fatta condizionando sui valori osservati per le feature di input tramite P(Y | X_s). Più variabili target possono essere modellate e imparate separatamente.
In sostanza, l’idea è, arriva un nuovo esempio, lo classifico trovando la distribuzione che massimizza P(X).
A differenza di altri modelli di apprendimento supervisionato, il NB può trattare esempi con dati mancanti, utilizzando l’assunzione missing at random, ovvero che la mancanza del valore è indipendente dalla classe e non influenza la classificazione.
NB è ottimale se si ha una sola feature osservata perchè non vanno fatte assunzioni di indipendenza, al crescere del numero di feature l’accuratezza dipende da quanto non indipendenti sono le variabili.
Se Y è booleana e X_i sono tutte osservate, allora NB = Regressione Logistica (i due modelli convergono agli stessi pesi), anche se NB apprende i parametri dalla stima MAP anche in caso di valori mancanti, la regressione logistica usa la discesa di gradiente che può tener conto di eventuali dipendenze ma non è applicabile in caso di valori mancanti perchè non posso applicare la sigmoide alla funzione lineare.
Per imparare un classificatore, le distribuzioni di P(Y) e P(X_i | Y) per ogni feature di input possono essere imparate dai dati. Ogni probabilità condizionata P(X_i | Y) può essere trattata come un problema separato per ogni Y, usando ad esempio le distribuzioni beta o Dirichlet.
Un caso semplice è la stima ML (alto bias, bassa varianza) dove P(X_i = x_i | Y = y) viene ottenuta come rapporto tra numero dei casi in cui X_i = x_i \land Y = y e quello dei casi in cui Y = y.
Prima della fase di apprendimento posso fare feature selection per individuare le feature predittive.
Le probabilità nulle possono avere effetti indesiderati, alcune feature diventano molto predittive perchè conoscere ad esempio un solo valore può tagliare fuori un’intera categoria, e un insieme finito di dati potrebbe essere insufficiente a fornire l’evienza necessaria per supportare una tale conclusione. Alcune combinazioni di osservazioni possono risultare impossibili, e quindi avere una divisione per zero nel classificatore, risolvibile con gli pseudo-conteggi.
In generale, il NB dà buoni risultati, è semplice, facile da implementare, e funziona bene se l’assunzione di indipendenza è appropriata.
Il NB può essere esteso con modelli in cui alcune X_i sono genitori e altre come figlie di Y, le probabilità della classificazione dati i genitori diventa rappresentabile con alberi di decisione, funzioni lineari o reti neurali, oppure considerando i figli di Y non necessariamente indipendenti, ma potrebbero avere un solo altro genitore oltre alla casse (purchè il grafo si mantenga aciclico).
1.2.2 Apprendimento MAP di alberi di decisione
La distribuzione a priori ci consente di stabilire un bias in favore di alberi più piccoli (quindi più semplici).
Se non ci sono esempi con gli stessi valori per le feature di input ma diversi valori per la feature target, ci sono sempre molteplici alberi di decisione che si adattano perfettamente ai dati. Per ogni assegnazione dei valori che non appare nel training set, ci sono alberi che si adattano perfettamente ma che fanno predizioni discordanti su esempi non visti. In tali casi, nessuno degli alberi che si adattano perfettamente al training set può risultare ottimale, quindi conviene scegliere anche tra quelli che si adattano meno perfettamente, consideriamo quindi che i dati sono affetti da rumore.
Per massimizzare il criterio MAP si passa ai logaritmi e si nega la quantità di informazione necessaria per descrivere gli esempi come descritti dal modello. Un modello che minimizza questa quantità è un modello dalla minima lunghezza di descrizione. Il principio MDL consiste nella scelta del modello che minimizza il numero di bit necessaria per descrivere sia il modello che gli esempi dato il modello: l’obiettivo è comunicare i dati nel modo più sintetico possibile. Per comunicare i dati, prima si comunica il modello, poi si comunicano i dati in termini del modello. Il numero di bit necessari per comunicare i dati utilizzando un modello è il numero di bit necessari per comunicare il modello più il numero di bit necessari per comunicare i dati in termini di modello.
Poiché la funzione logaritmo è monotonicamente crescente, il modello MAP è uguale al modello MDL. Scegliere un modello con la massima probabilità posteriore equivale a scegliere un modello con una lunghezza di descrizione minima.
Spesso è utile approssimare la lunghezza di descrizione del modello. Un modo per approssimare la lunghezza della descrizione è quello di considerare solo la rappresentazione dei parametri probabilistici del modello. Sia |t| il numero di parametri probabilistici del modello t. Per un albero decisionale con probabilità alle foglie, |t| è il numero di foglie. Per una funzione lineare o una rete neurale, |t| è il numero di parametri numerici.
Supponiamo che |E| sia il numero di esempi di addestramento. Ci sono al massimo |E|+1 probabilità diverse che il modello deve distinguere, perché la probabilità è derivata dai conteggi e nel set di dati possono esserci da 0 a |E| esempi con un particolare valore vero. Sono necessari \log_2(|E|+1) ≈ \log_2(|E|) bit per distinguere queste probabilità. Pertanto, il problema di trovare il modello MDL può essere approssimato a minimizzare
-\log_2 P(E ∣ t) + |t| \cdot \log_2(|E|)
Questo valore è il punteggio del criterio informativo bayesiano (BIC).
1.3 Apprendimento non supervisionato
Nell’apprendimento non supervisionato il training set è sprovvisto di feature-target, l’obiettivo è quello di ricostruire una classificazione naturale dei dati, pertanto attribuirò all’esempio un gruppo e non una classe. Un metodo generale per fare ciò è il clustering, dove partiziono gli esempi in cluster (classi naturali), dove ogni cluster predice i valori delle feature per gli esempi contenuti. Ogni cluster ha un errore di predizione associato (quanto un esempio è distante dal comportamento medio di quel cluster?), il clustering migliore è quello col minimo errore.
Vi sono due tipi di clustering: hard clustering e soft clustering:
Nell’hard clustering ogni esempio viene assegnato a un cluster preciso, il cluster può essere usato per predire i valori delle feature dell’esempio (k-means).
Nel soft clustering ogni esempio ha una distribuzione di probabilità di appartenenza ai cluster
1.3.1 K-means
E’ un algoritmo per l’hard clustering, riceve in input gli esempi di training e il numero di cluster k, richiede che i valori di ogni feature siano numeri, in modo che le differenze tra valori siano significative. Dà in output k cluster, dove ogni esempio è assegnato ad uno di essi.
Possiamo vedere il k-means come un risolutore di n problema di ottimizzazione teso a ottimizzare l’iperparametro k, ovvero il numero di cluster più adatto per dividere l’intero dataset.
Fine appunti, ora ti tocca usare le dispense/slide :(