11 Inductive Logic Programming (ILP)
11.1 Introduction to ILP
Inductive Logic Programming (ILP) merges logic programming (specifically first-order logic for formalism) with inductive learning (learning concept descriptions from examples). It performs inference from specific observations to derive general hypotheses.
11.1.1 Core Idea
The learning process in ILP can be characterized as:
Given:
- Input Knowledge (I)
- Goal (G)
- Background Knowledge (BK)
- Transmutations (set(T)) - Operators that change knowledge
Determine:
- Output knowledge (O), that satisfies G, by applying transmutations from T to I and BK.
This process is viewed as a goal-driven search in a knowledge space defined by the representation language and search operators.
11.1.2 Advantages of ILP
- Unified Formalism: Uses the same logic-based formalism for data, hypotheses, and background knowledge.
- Expressive Power: High capability to represent complex concepts.
- Human-Readability: Resulting hypotheses are often understandable.
- Background Knowledge Integration: Allows explicit inclusion of domain knowledge.
- Powerful Reasoning: Leverages established mechanisms from logic theory.
11.2 Foundations of Learning in ILP
11.2.1 Types of Inference
A general formula for inference is: P \cup B \vdash C
- P: Premise
- B: Background knowledge
- C: Consequence
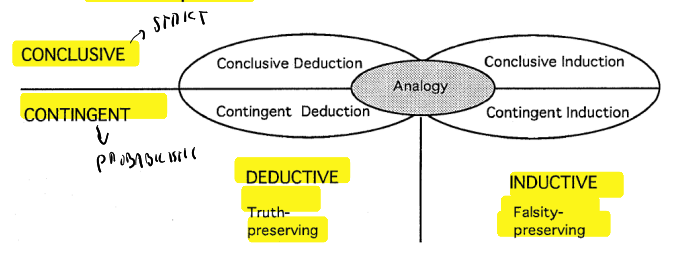
11.2.2 Induction in Logics
Given a set of sentences representing beliefs, with a subset as data (\Delta) and the rest as background theory (\Gamma): If \Gamma \not\vdash \Delta (the theory doesn’t explain the data), then \Phi is an inductive conclusion (\Gamma \cup \Delta \vdash \Phi) iff:
- \Gamma \cup \Delta \not\vdash \neg\Phi: The hypothesis \Phi is consistent with \Gamma and \Delta.
- \Gamma \cup \Phi \vdash \Delta: The hypothesis \Phi explains the data \Delta.
In logical terms, given consistent observations (O) and background knowledge (B), find a hypothesis (H) such that B \land H \vdash O: the background knowledge and the hypothesis logically prove the observations.
11.2.3 The ILP Learning Task
Given:
- A set of observations O:
- Positive examples E+
- Negative examples E-
- Background knowledge B
- Language of hypotheses LH
- Covering relationship (defines how H explains examples)
Find:
- A Hypothesis H \in LH such that, given B,
- H covers all positive examples (Completeness)
- H covers no negative examples (Consistency)
In ILP, examples are typically ground facts, and B and H are sets of definite clauses.
11.3 ILP as a Search Problem
The search space in ILP is determined by the language of logic programs (L), where states are concept descriptions (hypotheses). The goal is to find one or more hypotheses satisfying the completeness and consistency criteria.
11.3.1 Structuring the Search Space: Generality
The hypothesis space is structured by a generality relationship: G is more general than S iff covers(S) \subseteq covers(G).
Pruning the search space:
- Positive examples: If H covers an example E, then all generalizations of H also cover E.
- Negative examples: If H does not cover an example E, then no specializations of H will cover E.
11.3.2 Ordering Relations for Clauses
Understanding ordering is key to navigating the search space. Given a set of clauses S, and C, D, E \in S:
- Quasi-ordering (\leq): Reflexive (C \leq C) and transitive (C \leq D \land D \leq E \Rightarrow C \leq E).
- Partial ordering: A quasi-ordering that is also anti-symmetric (C \leq D \land D \leq C \Rightarrow C = D).
- Total ordering: For any pair C, D, either C = D, C \leq D, or C \geq D.
11.4 Generalization Relationships in ILP
Clauses can be ordered using generalization relationships: implication (\Rightarrow), \theta-subsumption (\leq_{\theta}), and \theta_{OI}-subsumption (Object Identity).
11.4.1 Implication (\Rightarrow)
- Definition: C is more general than D (C \Rightarrow D) if whenever C is true, D is also true.
- Properties:
- Undecidable: No general procedure exists to decide if D \Rightarrow C.
- Quasi-ordering: Not a partial ordering (anti-symmetry doesn’t hold; non-renaming clauses can be equivalent).
- Least General Generalization (lgg):
- A clause C is a generalization under implication of S = {D_1, …, D_n} iff \forall i: C \Rightarrow D_i.
- C is an lgg of S if for any other generalization C’ of S, C’ \Rightarrow C.
- The lgg of a finite set of clauses is not computable (implication is undecidable) and not unique under implication (because of the quasi-ordering).
11.4.2 \theta-Subsumption (\leq_{\theta})
- Definition: C \theta-subsumes D (C \leq_{\theta} D) iff there exists a substitution \theta such that C\theta \subseteq D (all literals in C\theta are in D).
- Properties:
- Decidable: A procedure exists, but the test is generally NP-complete.
- Quasi-ordering: Not a partial ordering (not anti-symmetric).
- Weaker than implication: Lacks the ability to handle recursion in the same way.
- Lattice Structure: The set of clauses (C, \leq_{\theta}) forms a lattice with:
- \land_{C} (glb): Most specific generalization under \theta-subsumption.
- \lor_{C} (lub): Most general specialization under \theta-subsumption.
- The lattice structure admits infinite chains of syntactically different but equivalent clauses, potentially causing non-termination in search.
- Unique lgg: The lgg under \theta-subsumption is unique.
11.4.2.1 Calculating lgg under \theta-Subsumption
- Terms t_1, t_2:
- lgg(t, t) = t
- lgg(f(s_1, …, s_n), f(t_1, …, t_n)) = f(lgg(s_1, t_1), …, lgg(s_n, t_n))
- lgg(f(s_1, …, s_n), g(t_1, …, t_m)) = V (where f \neq g, V is a new variable)
- lgg(s, t) = V (where s \neq t, and at least one is a variable, V is a new variable)
- Atoms a_1, a_2 (same predicate p):
- lgg(p(s_1, …, s_n), p(t_1, …, t_n)) = p(lgg(s_1, t_1), …, lgg(s_n, t_n))
- lgg(p(…), q(…)) is undefined if p \neq q.
- Literals l_1, l_2:
- Positive: lgg(a_1, a_2) as above.
- Negative (\nega_1, \nega_2): lgg(\nega_1, \nega_2) = \neglgg(a_1, a_2).
- Opposite signs: Undefined.
- Clauses C_1 = {h_1, …, h_n}, C_2 = {k_1, …, k_m}:
- lgg(C_1, C_2) = {l_{ij} = lgg(h_i, k_j) | h_i \in C_1, k_j \in C_2 \land lgg(h_i, k_j) is defined}
A key issue with \theta-subsumption is that distinct variables can be substituted by the same term.
11.4.3 \theta_{OI}-Subsumption (Object Identity)
This addresses some limitations of \theta-subsumption by assuming that terms denoted by different symbols in a clause must be distinct.
- Definition: C \theta_{OI}-subsumes D iff \exists a substitution \alpha such that C_{OI}\alpha \subseteq D_{OI}.
- Properties:
- Weaker than \theta-subsumption.
- Anti-symmetric: Only renamings can be equivalent (unlike \theta-subsumption or implication).
- Quasi-ordered set: Reflexive and transitive.
- Not a lattice: Unlike \theta-subsumption, different LGGs can be incomparable.
- Redundancy test complexity: O(n^2).
- Each element in the space is an equivalence class.
11.5 Refinement Operators
Refinement operators (generalization and specialization) are used to navigate the structured search space.
11.5.1 Properties of Ideal Refinement Operators
- Local finiteness: Ensures computation terminates for each step.
- Properness: Avoids loops on the same refinement (generates distinct clauses).
- Completeness: Capable of reaching any refinement from any clause.
- Optimality: Provides a single, unique path to any refinement.
11.5.2 Existence of Ideal Operators
- Do not exist under \theta-subsumption.
- Do exist under Object Identity (\theta_{OI}-subsumption).
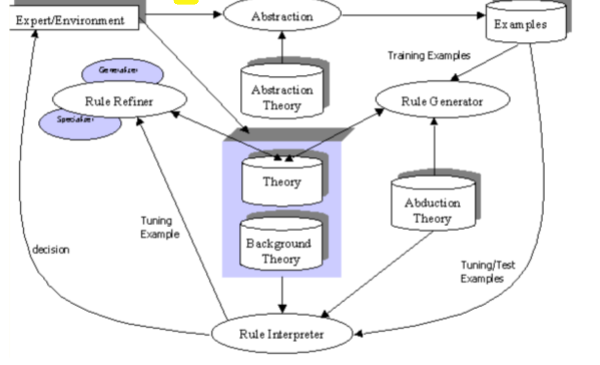
11.6 Example System: InTheLEx (Incremental Theory Learner from Examples)
InTheLEx is an ILP system with the following characteristics:
- Fully incremental: Learns from examples one by one.
- Multi-conceptual: Can learn multiple concepts.
- Closed-loop feedback: Incorporates learned knowledge.
- Hierarchical theories: Can learn structured knowledge.
- Handles Positive and Negative examples.
- Total storage: Retains all information.
- Multi-strategy: Employs various reasoning techniques.
- Based on Object Identity.