4 Representation
Categorization is the procedure of organizing objects into classes or categories. It allows defining properties and making assumptions about the entire category rather than individual elements. The choice of categories determines what can be represented.
Humans organize concepts into 3 hierarchical levels:
- Basic concepts: the natural way to categorize objects and entities that make up our world
- Subordinate concepts: specialization
- Superordinate concepts: generalization
Once formed, categories tend to have a structure that stresses the similarity among members of the same category and maximizes the differences between members in different categories. This allows reasoning with prototypes. This is reminiscent of the clustering process. This is useful because it is easier to reason with a prototype than with all the members of a category: much reasoning happens at the category level, rather than for individuals.
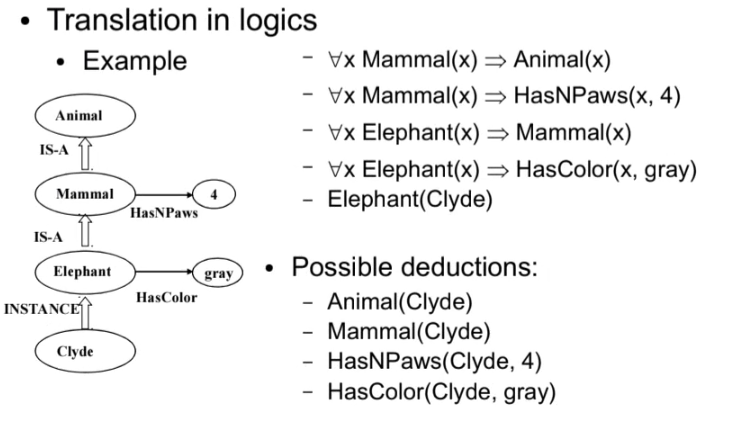
If knowledge is organized into categories, it is sufficient to classify an object by its properties to infer the properties of the category it belongs to, using inheritance as a form of inference. Inheritance is the characterization of a property A given at the class level but interpreted as a property of all instances of the class: \forall x (is\_a(x, Class) \Rightarrow A(x)). This is a graph search: starting from the given node, a bottom-up search in the taxonomy is performed for a node defining its properties.
What typically characterizes a concept are:
- Necessary conditions, guaranteed to be true
- Bird(x) \Rightarrow Vertebrate(x)
- Bird(x) \Rightarrow Biped(x)
- Typically necessary conditions (default)
- Bird(x) \Rightarrow_{Tip} Flies(x)
- Bird(x) \Rightarrow_{Tip} Feathered(x)
- Sufficient conditions (criterial) to implement generalization/specialization relationships
- Canary(x) \Rightarrow Bird(x)
- Ostrich(x) \Rightarrow Bird(x)
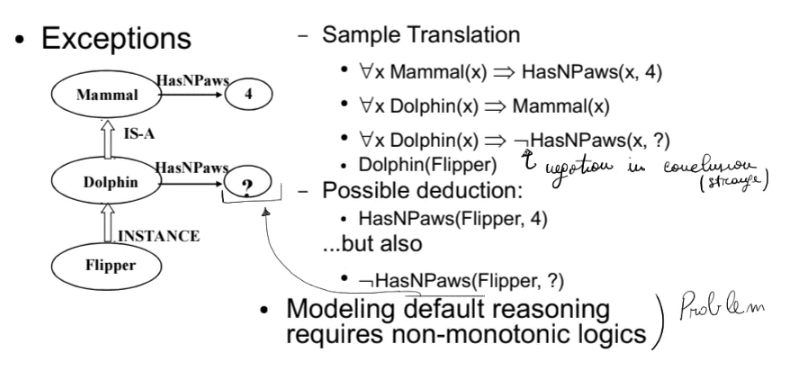
- Typically sufficient conditions, admitting exceptions
- Flies(x) \land Tweets(x) \Rightarrow_{Tip} Bird(x)
- Feathered(x) \Rightarrow_{Tip} Bird(x)
Typicality requires logic different from traditional logic to handle exceptions. In fact, in traditional logic, the monotonicity property holds: if a conclusion is valid, adding more premises does not invalidate it; instead, the set of possible conclusions increases. With typicality, this is not true: adding a typicality condition can invalidate a conclusion. For example, if we know that all birds fly, and we add the information that penguins are birds, we cannot conclude that penguins fly.
4.1 Knowledge Representation Schemes
- Graphs: Formal structures of nodes and arcs, representing entities and their relationships.
- Frames: Data structures for stereotypical concepts and objects, representing static knowledge.
- Scripts: Data structures for typical sequences of events, representing dynamic knowledge.
4.2 Graph-Based Representations
Graphs are fundamental for analyzing knowledge in terms of low-level primitives and organizing it into high-level structures. They represent common-sense knowledge using nodes for concepts and arcs for relationships, allowing for the definition of inferences through these connections.
4.2.1 Sowa’s Conceptual Graphs
Conceptual graphs are a method to represent mental models. They have 2 kinds of nodes: concepts (concrete or abstract) and relationships (part-of, object-of, …). The relationship node explains the dependence between concepts. We can see them as labeled graphs where the label is defined by the relationship node.
This representation is able to formally detect how what we think about a concept can be described in terms of its relationships with other kinds of concepts. The power lies in the capacity to formalize both concrete and abstract concepts, along with hierarchies of concepts and the ease of representing mental models.
4.2.2 Semantic Networks
Semantic Nets got their name because their primary, original purpose was to model and understand the meaning (semantics) found in spoken or written language.
A distinctive feature behind semantic nets is “cognitive economy”. This term refers to the idea of storing information efficiently to minimize redundancy, much like how human memory is thought to work.
They can be more broadly called Associative Nets because the underlying structure can be used for many other types of knowledge beyond just language.
A Semantic Net is a Labeled Directed Graph where nodes are objects, situations, or actions, and arcs are binary relationships. They are based on the graphical representation of the relationships existing between elements in a given domain, and they can be reduced to a tractable symbolic representation (logics). Constraints are represented on features. Nodes can be token-nodes as individual physical symbols (instances), or type-nodes, as sets of symbols (classes).
The basic idea is that the meaning of a concept is determined by its relationships with other objects. Information is stored by interconnecting nodes (entities) with labeled edges (relationships).
Typical relationships are is-a (subclass), part-of (part-whole), has, value, and some linguistic relationships.
What about n-ary relationships (n > 2)? Reification is a common technique, where the relationship itself is turned into a node.
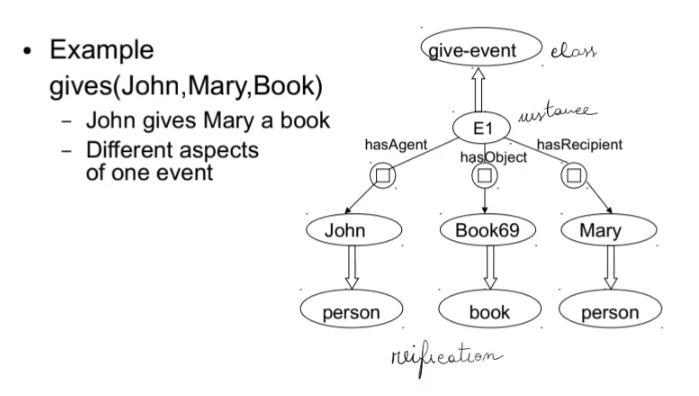
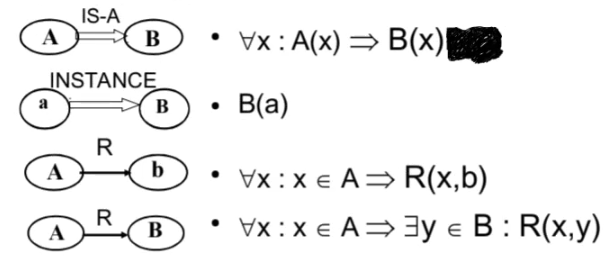
Semantic Nets are a comfortable notation for a portion of First-Order Logic. The problem with basic semantic nets is modeling default reasoning, which requires non-monotonic logics.
4.2.2.1 Inference in Semantic Networks
The following are two methods to perform inference in semantic networks:
- Search for intersection:: a form of spreading activation starting from two nodes:
- Label a set of source nodes (concepts) with weights (activations).
- Iteratively propagate these activations from the source nodes to linked nodes.
- Relationships among objects are found by expanding activation from the two source nodes and identifying their intersection. This intersection is typically found by assigning a special tag to each visited node during the expansion from each source.
- Inheritance: Based on is_a and instance links and exploiting the transitivity of is_a. It is easily implemented as link traversal.
4.3 Frames
Frames extend graph-based approaches to represent knowledge in more structured ways.
4.3.1 From Semantic Nets to Frames
Semantic Nets are unsuitable for complex domains, as most links represent very general relationships and are unable to capture the complex semantics of real-world problems. The subsequent focus was the definition of a richer set of labeled links useful for modeling the semantics of natural language. This led to the definition of frames.
Frames are data structures used to represent stereotypical situations and typical objects in a meaningful representation. We can think of frames in semantics and computational linguistics as a schematization of a situation, state, or event using lexical units that recall the situation or event (e.g., words “buy”, “sell”, “cost”) and using semantic roles (e.g., “buyer”, “seller”, “money”).
The idea is to invoke a known situation to give meaning to a sentence or situation, a technique already used in natural language understanding. In this way, we can “emulate” long-term memory, activating many frames to understand complex situations and to find plausible justifications for situations not corresponding to the expectations of the activated frames.
Frames encode a set of expectations that guide understanding by providing context. The goal is to represent these expectations algorithmically, enabling a computer to leverage implicit knowledge and make inferences about sequences of events, similar to how humans derive meaning from coherent narratives.
4.3.2 Frame Structure
Frames are typically composed of:
- A name
- A set of slots (attribute-value pairs), where the attribute is the slot’s name and the value is the slot’s filler.
- In this way, we can embed relationships between different frames and an inheritance hierarchy (specialization slot a-kind-of).
- A set of fillers (values) for each slot, which can include:
- Frame name (for nested frames or relationships)
- Frame relationships to other frames
- Slot actual value (symbolic, numeric, boolean)
- Slot default value
- Slot range of values (or restrictions on values)
- Procedural information: instructions to be executed, which may drive the reasoning process using IF-THEN rules that activate an associated process. These are often called demons or procedural attachments:
- IF-ADDED rules: activated whenever a slot’s value changes. This triggers a forward inference rule, from premises to conclusions.
- IF-NEEDED rules: activated on request when a slot’s value needs to be determined. This triggers a backward inference rule, similar to Prolog, starting from a goal and looking for rules or facts about it.
When considering a specific situation, a copy of the general frame (instantiation) is made and added to short-term memory. The slots of this instance are then filled with specifications of the particular situation.
4.3.3 Inheritance in Frames
Frames support inheritance through specialization links (e.g., is-a, a-kind-of). Sub-frames inherit slots and values from their super-frames, but can also override them or add new ones.
4.3.4 Frame System Representation
A frame system can be thought of as a network of nodes and relationships. Individual frames are nodes, and relationships between slots (and thus between frames) are arcs.
4.3.5 Reasoning with Frames
When facing a new situation, a relevant frame is selected from memory, and its details are adapted as needed. Each frame is associated with several types of information: how to use the frame, what one might expect to happen next, and what to do if these expectations are not confirmed.
The core inference mechanism is often matching: a new situation (or frame instance) is understood by matching it against existing frame definitions. A frame instance can be considered an instance of a more general frame if the former matches the latter.
When a frame is not suitable to a situation it can be transformed, applying small changes, or replaced for significant changes: look for new frames whose terminal slots correspond to a sufficient number of terminal slots of the original frame.
4.3.6 Primitives for Frame Systems
Common operations in a frame-based system include:
- Invocation: initial consideration of a frame.
- Determination: deciding if there is enough evidence to infer an invoked frame.
- Processing: filling a slot of a given frame.
- Termination: inferring that a given frame is not relevant anymore.
4.4 Scripts
Scripts represent knowledge about stereotyped sequences of events. They are built upon the idea of conceptual dependency.
4.4.1 Conceptual Foundation and Purpose
Conceptual dependency is a theory on how to represent knowledge about events, usually contained in natural language sentences. It is a mechanism to represent and reason about events. The aim is to represent knowledge in a way that facilitates easy inference from sentences and is independent of the original language. This is achieved by representing actions as a set of primitive actions.
A script is a structure composed of a set of slots. Scripts are used to create expectations about event sequences and to notice deviations from those expectations. Scripts are based on the fact that event sequences possess a logical, causal, and temporal structure. A causal chain among events can be represented using a script.
4.4.2 Script Structure
A script is typically made up of:
- Entry conditions: conditions that must be satisfied before the events described in the script can occur.
- Result: conditions that are true after the events described in the script have taken place.
- Props: objects involved in the events.
- Roles: subjects and individuals involved in the events.
- Trace: a variant or particular accepted meaning of a more general scheme (script).
- Scenes: the actual sequences of events that occur.
4.4.3 Script Activation
There are two ways to activate a script:
- Temporary scripts: scripts that are mentioned or referenced but are not fundamental to the main narrative.
- These are not central to the description. For instance, in “While going to the museum, Susan passed by a restaurant. She greatly enjoyed the Picasso exhibition,” the restaurant script is not central but might be activated later via a pointer.
- Non-temporary scripts: scripts that are central to the description and must be completely activated.
4.4.4 Advantages of Scripts
- They allow for the prediction of events not explicitly observed.
- They provide a means for building a consistent interpretation from a set of observed facts.
- They allow focusing on unusual events, highlighting where the description of observed facts diverges from the standard sequence of events.