12  Multi-Strategy Reasoning

Multi-Strategy Reasoning (MSR) in Artificial Intelligence involves combining various reasoning techniques to solve complex problems that may not be efficiently or effectively solvable by a single method. By integrating approaches like abstraction, abduction, argumentation, and analogy, MSR systems aim to leverage the strengths of each strategy, leading to more robust, flexible, and powerful problem-solving capabilities.

12.1 Abstraction

Abstraction is a cognitive process that enhances problem-solving efficiency by selectively focusing on essential information while discarding irrelevant details. This process is goal-driven and subjective, requiring a careful balance: excessive abstraction can obscure critical details needed for a solution, whereas insufficient abstraction may not yield significant efficiency gains.

In any reasoning scenario, concrete objects exist in the underlying world of experience. However, our access to this world is mediated by perception. For this discussion, we will consider static situations where the world does not change over time.

Key components in understanding abstraction include:

1. Perception (P(W)): An observer’s perception of the world (W). This is the primary source of information, representing the world with some inherent loss of detail. It can be compared to feature selection in machine learning.
2. Structure (S): To make perceived stimuli available over time, they must be memorized into an organized structure. S typically consists of tables that group objects sharing common properties, effectively forming a relational database that exhaustively encodes attribute values, functions, and relations. Each physical object is assigned a unique identifier. While S describes the world extensionally (listing facts), an intensional (rule-based) description is also often needed.
3. Language (L): A formal language is necessary to reason about the perceived world and to communicate with other agents. The semantics of L are evaluated based on the tables in S.

The reasoning context can thus be defined as R = (P(W), S, L).

Consider a world W and a perception system P(W) composed of sensors, each dedicated to receiving specific signals and equipped with a distance measure to distinguish them. A signal pattern (or configuration) is a set of values provided by these sensors. Let \Gamma be the set of all possible configurations.

If P_1(W) and P_2(W) are two perception systems for W, with configuration sets \Gamma_1 and \Gamma_2 respectively, P_2(W) is considered simpler than P_1(W) if:

• There exists a function f: \Gamma_1 \rightarrow \Gamma_2 such that any configuration \gamma_1 \in \Gamma_1 uniquely determines a configuration \gamma_2 \in \Gamma_2.
• The inverse function f^{-1} does not exist, meaning information removed during simplification cannot be recovered. A simpler perception system, P^{'}(W), offers the observer less information to manipulate.

Abstraction is formally a functional mapping A: P_g(W) \rightarrow P_a(W). This maps a ground perception P_g(W) (containing all details) to a simpler abstract perception P_a(W) (with fewer details) of the same world W. While function A allows any abstract configuration to be uniquely determined from a ground one, the reverse is not true. Abstractions can be theorem-increasing (allowing more theorems to be proven in the abstract space) or theorem-decreasing, depending on their properties relative to the ground world.

P(W) can be conceptualized as a tuple (OBJ, ATT, FUNC, REL):

• OBJ: A set of perceived objects.
• ATT: A set of object attributes.
• FUNC: A set of functional links between objects or attributes.
• REL: A set of relations between objects.

12.1.1 Scheme of the Abstraction Process

Abstraction operators, denoted by P, S, and L, act at the perception, structure, and language levels, respectively. These operators transform representations from a ground level to an abstract level.

The available operators at each level are analogous:

• Perception Level P(W): \Omega = { \omega_{ind}, \omega_{ta}, \omega_{hide}, \omega_{eq-val}, \omega_{red-arg}, \omega_{prop} }
• Structure Level S: \Phi = { \phi_{ind}, \phi_{ta}, \phi_{hide}, \phi_{eq-val}, \phi_{red-arg}, \phi_{prop} }
• Language Level L: \Lambda = { \lambda_{ind}, \lambda_{ta}, \lambda_{hide}, \lambda_{eq-val}, \lambda_{red-arg}, \lambda_{prop} }

Common types of abstraction operators include:

• Indistinguishable Objects (\omega_{ind}, \phi_{ind}, \lambda_{ind}): Groups objects that are considered the same into equivalence classes.
  • Arguments: A set of objects (OBJ) to be treated as indistinguishable.
• Term Abstraction / Compound Object Creation (\omega_{ta}, \phi_{ta}, \lambda_{ta}): Groups a set of ground objects to form a new compound object.
  • Arguments: A set of objects (OBJ). The original “primitive” objects disappear from the abstract representation.
• Hiding Details (\omega_{hide}, \phi_{hide}, \lambda_{hide}): Ignores certain aspects of the world.
  • Arguments: Subsets of OBJ, ATT, FUNC, or REL to be ignored.
• Equivalent Values (\omega_{eq-val}, \phi_{eq-val}, \lambda_{eq-val}): Merges subsets of values for attributes, functions, or relations.
  • Arguments: Subsets of values within OBJ, ATT, FUNC, or REL. If values belong to a function’s range, this can approximate the function.
• Argument Reduction (\omega_{red-arg}, \phi_{red-arg}, \lambda_{red-arg}): Reduces the arity (number of arguments) of a function or relation by dropping specified arguments.
  • Arguments: A function/relation and a subset of its arguments.
• Propositionalization (\omega_{prop}, \phi_{prop}, \lambda_{prop}): Eliminates all arguments of a function or relation, effectively moving from predicate logic to a propositional logic representation.
  • Arguments: Subsets of FUNC or REL.

12.2 Abduction

Abduction is a reasoning process aimed at inferring the most plausible explanation for a given set of observations. It is particularly prevalent in diagnostic tasks, where the objective is to identify the likely cause(s) of observed symptoms. The process typically involves generating potential hypotheses that could account for the observations and then selecting the most credible one(s).

Consider the relationship: BackgroundKnowledge \cup Theory \vdash Conclusion. The roles of abduction, deduction, and induction can be framed as follows:

• Abduction: Given a Theory and an observed Conclusion, abduction infers the specific Background Knowledge (or facts) that would explain the Conclusion.
• Deduction: Given Background Knowledge and a general Theory, deduction aims to derive a specific Conclusion or prediction.
• Induction: Given Background Knowledge and a desired Conclusion, induction aims to establish the Theory that logically connects them.

Abduction primarily infers extensional knowledge (specific facts) relevant to a particular scenario. In contrast, induction typically infers intensional knowledge (general rules) that hold across various situations.

For instance, if a car fails to start, an abductive explanation might be that its battery is dead. An inductive inference, on the other hand, would be to derive the general rule “if the battery is empty, then the car will not start” from multiple instances of this co-occurrence.

12.2.1 Abductive Logic Programming (ALP)

Abductive Logic Programming provides a formal framework for abduction, typically defined by a triple (P, A, IC):

• P (Program): A logic program (e.g., in Prolog).
• A (Abducibles): A set of ground (variable-free) atomic formulas, termed abducibles. These are potential hypotheses. No predicate p \in A can appear in the head (conclusion part) of a rule in P.
• IC (Integrity Constraints): A set of logical formulas that must be satisfied by any valid interpretation of the abducibles. These constraints ensure consistency and plausibility.

Given an ALP theory (P, A, IC), an abductive explanation for a query Q is a set \Delta \subseteq A of ground abducible atoms such that:

1. P \cup \Delta \vdash Q (The program P, augmented with the abduced facts \Delta, logically entails the query Q).
2. P \cup \Delta \models IC (The program P, augmented with \Delta, satisfies all integrity constraints IC).
3. P \cup \Delta is consistent.

The set \Delta represents a collection of assumed states of affairs under which the query Q (the explanation target) would hold true, thus constituting an abductive solution.

12.2.2 How to Carry Out Abductive Inference

Two main procedures are involved in abductive inference within ALP:

1. Abductive Derivation: This extends standard Logic Programming derivation (like Prolog’s resolution). When an abducible atom is needed to satisfy a goal:
   • If it has not already been abduced (nor has its negation), it can be tentatively abduced.
   • This tentative abduction is confirmed only if the Consistency Derivation (see below) succeeds, ensuring that integrity constraints are met.
2. Consistency Derivation: This procedure checks whether all integrity constraints (ICs) involving the currently abduced set \Delta are satisfied. To do this, it may need to determine the truth or falsity of other atoms present in the ICs, potentially by invoking further Abductive Derivations.

12.2.3 Expressive ALP

The basic ALP framework can be enhanced by incorporating additional types of constraints, often associated with logical operators:

• Standard logical connectives: nand, xor, or, and, nor.
• Conditional constraints:
  • if([l_1, …, l_n], [l_1^{'}, …, l_m^{'}]): If all literals l_1, …, l_n are true, then all literals l_1^{'}, …, l_m^{'} must also be true (modus ponens). Conversely, if at least one literal l_1^{'}, …, l_m^{'} is false, then at least one literal l_1, …, l_n must be false (modus tollens).
  • iff([l_1, …, l_n], [l_1^{'}, …, l_m^{'}]): Either all literals in both sets ([l_1, …, l_n] and [l_1^{'}, …, l_m^{'}]) are true, or at least one literal in each set is false.

12.2.4 Probabilistic Expressive ALP

This extension introduces probabilities into the ALP framework, defined by a 4-tuple (P, A, I, p):

• P: A standard or probabilistic logic program.
• A: A set of abducible predicates.
• I: A set of integrity constraints.
• p: A function p: P \cup ground(A) \cup I \rightarrow [0,1] that assigns a probability (referred to as strength) to each rule in P, each ground abducible literal in ground(A), and each integrity constraint in I. Elements not explicitly assigned a probability are assumed to have a probability of 1.

Given an abductive explanation E, which consists of a set of rules from P used in the derivation (L), the set of abduced literals (\Delta), and the set of relevant integrity constraints (C), its likelihood p(E) is calculated as:

p(E) = \prod_{l \in L} p(l) \cdot \prod_{\delta \in \Delta} p(\delta) \cdot \prod_{c \in C} p(c)

The most likely explanation is the one that maximizes this probability p(E).

12.3 Argumentation

Argumentation is a reasoning paradigm focused on identifying, analyzing, and evaluating arguments. It offers structured procedures for making and justifying decisions, especially in situations involving doubt or conflicting information. The core idea is to provide reasons (arguments) to support claims and to defend these claims against counter-arguments (attacks).

An argument is a set of propositions from which a conclusion can be inferred. It represents an attempt to persuade by providing reasons for accepting a conclusion as valid or evident.

12.3.1 Types of Argumentation

1. Structured Argumentation: Involves complex arguments, often represented as trees of statements with an explicit logical structure. The internal content and construction of arguments are central.
2. Abstract Argumentation: Focuses on the relationships between arguments, abstracting away their internal structure. Arguments are treated as atomic entities.
   • This is often visualized as a directed graph where nodes represent arguments (claims) and arcs represent an “attack” relation (e.g., an arc from A to B means A attacks B).
   • The primary strategy is to identify sets of arguments that can “survive the conflict together” known as extensions.

12.3.1.1 Extension-based Semantics in Abstract Argumentation

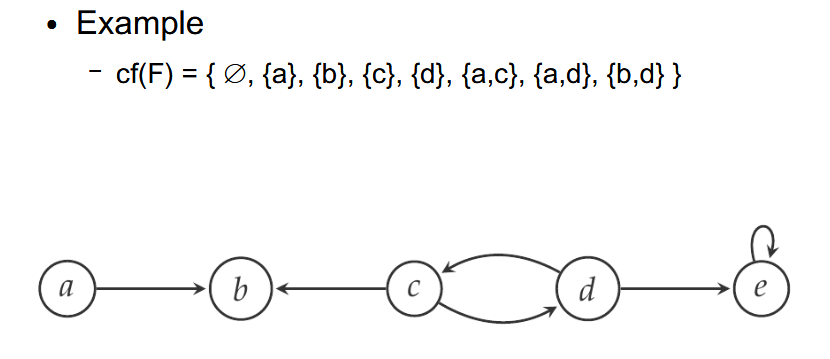
A fundamental property for an acceptable set of arguments is conflict-freeness.

• Conflict-Free Set: Given an Argumentation Framework (AF) f = (A, R), where A is a set of arguments and R is an attack relation (a R b means ‘a attacks b’), a subset S \subseteq A is conflict-free if no argument in S attacks another argument in S (i.e., \not\exists a, b \in S such that a R b). This is a basic requirement for any coherent set of arguments.

Building upon conflict-freeness, other important properties define various semantics:

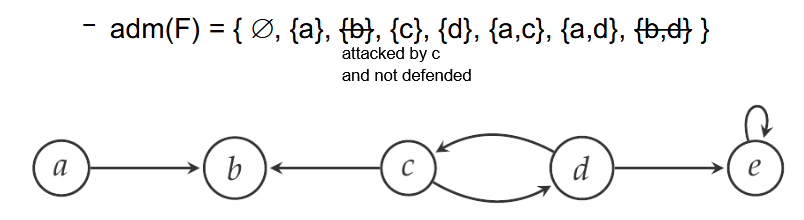
• Admissibility: A conflict-free set S should be able to defend itself against external attacks.
  • S \subseteq A is admissible if S is conflict-free, and S defends all its members. That is, for every argument a \in S and every argument b \in A such that b attacks a (b R a), there must exist an argument c \in S such that c attacks b (c R b).

12.3.2 Ranking-based Semantics

An alternative to extension-based approaches, ranking-based semantics assign a degree of acceptability to each argument rather than making a binary accepted/rejected decision.

Feature	Extension-based Semantics	Ranking-based Semantics
Acceptability	Arguments are either accepted or rejected	Gradual levels of acceptability assigned
Defeated Arguments	Typically “killed” or entirely excluded	Arguments are weakened, possibly extremely
Impact of Attacks	Number of attacks often irrelevant beyond the first	More attacks generally mean less acceptable

12.3.3 Limitations of Basic Abstract Argumentation

• They primarily support a symbolic representation of knowledge (propositions and attack relations).
• They often neglect social aspects (e.g., trust in arguers), preferences between arguments, or varying strengths of attacks.
• Attacks are typically binary (present or absent), without weights.

These limitations can be addressed by several variants and extensions.

12.3.4 Advanced Argumentation Frameworks

1. Bipolar Argumentation Frameworks (BAFs):
   • Extend AFs by introducing a second relation: support.
   • Arguments can attack or support other arguments. Support is often considered transitive.
   • This allows for more complex interactions, such as “supported attacks” (an argument supports an attacker) or “indirect attacks” (an argument attacks a supporter).
2. Weighted Argumentation Frameworks (WAFs):
   • Assign weights to attacks, often representing measures of inconsistency or the strength of the attack.
   • Weights can be used to, for example, remove weaker attacks up to a certain threshold of tolerated incoherence, thereby altering the resulting extensions.
3. Bipolar Weighted Argumentation Frameworks:
   • Combine features of BAFs and WAFs.
   • Relations (both attack and support) are assigned weights, typically in a range like [-1, 1]:
     • Values in [-1, 0) represent attacks (strength increasing towards -1).
     • Values in (0, 1] represent supports (strength increasing towards 1).
     • 0 indicates no direct relationship.

12.4 Analogy

Analogy is a cognitive process involving the transfer of knowledge and inferences from a familiar domain (the source) to a less familiar one (the target). The core idea is to identify structural similarities between the two domains and use these similarities to guide understanding or problem-solving in the target domain.

The process of analogical reasoning is often described in several steps:

1. Retrieval: Identifying and accessing a suitable source domain from memory that is potentially analogous to the target domain.
2. Mapping: Establishing correspondences between elements (objects, attributes, relations) of the source and target domains.
3. Evaluation: Assessing the quality and validity of the established mapping. This involves criteria like structural consistency and plausibility.
4. Transfer/Inference: Using the mapping to transfer knowledge or draw new inferences about the target domain based on knowledge from the source domain.
5. Pattern Completion/Adaptation: Shifting or adjusting the representation of one or both domains to improve the alignment and converge towards a common analogical pattern.
6. Re-representation: Modifying parts of the representation of either the source or target (or both) to enhance the match and facilitate the analogical transfer.

Argumentation techniques can be employed in the context of analogy, for instance, to help identify and evaluate candidate mappings. By treating potential correspondences as claims and conflicts between them as attacks, conflict-free sets of mappings could represent consistent analogical interpretations.