14  Modal Logics

We can extend or modify classical logic. The assumptions we made with Predicate Logic Reasoning are the following:

• Each fact is either true or false; we operate under Closed World Assumptions.
• Knowledge must be consistent, while in human reasoning, alternative hypotheses are considered and are removed as soon as new evidence is available.
• Knowledge monotonically grows through the use of inference rules.

Modal logics are a family of extensions of logics:

• Temporal
• Deontic
• Epistemic
• Alethic
• Ethic

14.1 Temporal Logics

Extend classical logic with operators such as:

• \square A: “A is always true”
• \lozenge A: “A is sometimes true”
• \bigcirc A: “A is true in the next state”

We can “simulate” these operators in traditional logic using moments as arguments, but we must include an arithmetic structure to handle the temporal aspects.

Example

“the train to Rome is leaving”

[\neg leave(train, rome)] \Rightarrow [\bigcirc \neg leave(train, rome)]

• If the train to Rome is not leaving now, then it will leave in a moment.

Simulation:

• \neg leave(0, train, rome) \Rightarrow leave(1, train, rome)

14.2 Deontic Logics

Allows expressing obligation or permission, with operators such as:

• OA: A is mandatory
• PA: A is permitted
• O \neg A: A is forbidden

Axioms:

• PA \iff \neg O \neg A: all and only non-prohibited things are permitted
• OA \Rightarrow PA: what is mandatory must be permitted

14.3 Epistemic Logics

Allows working on a meta-level (meta-knowledge and meta-reasoning), modeling knowledge and beliefs, with operators such as:

• K: denotes what an agent knows
  • A: the agent knows that proposition A is true
• B: denotes what an agent believes
  • A: the agent believes that proposition A is true

Examples

K \exists x thief(x, C): the agent knows that someone stole the picture.

\exists x K thief(x, C): the agent knows who stole the picture.

This allows representing what agents know or believe about each other, hence the meta-level.

Example

K(\alpha, A) \iff K_{\alpha}(A): agent \alpha knows that A is true

B_{\alpha}(A): agent \alpha believes that A is true

K_{\alpha}(A) K_{\beta}(A): agent \alpha knows that agent \beta knows that A is true

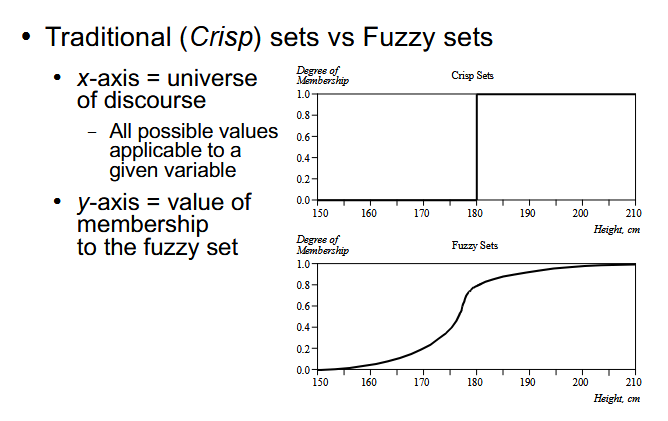
14.4 Fuzzy Theory

Fuzzy theory is a mathematical theory that encodes qualitative evaluations. It is an extension of Boolean logics to values in the continuous range [0, 1]. It is based on the idea that the elements of a set are defined through a degree of membership.

The degree of membership can be interpreted as a probability, and many kinds of membership functions are available, with the only requirement being smooth functions to model the uncertainty.

14.4.1 Operations

• Complement: \mu_A(x) = 1 - \mu_A(x)
• Intersection: \mu_{A \cap B}(x) = min(\mu_A(x), \mu_B(x))
• Union: \mu_{A \cup B}(x) = max(\mu_A(x), \mu_B(x))

14.5 Non-monotonic reasoning

• Default logic
• Negation as failure