13  Similarity

We want to find how to measure similarity between Horn clauses.

Given:

• m: number of features of i not present in j
• l: number of features in common between i and j
• n: features of j not present in i
• \alpha \in [0, 1]: relative imporrtante of i with respect to j

sf(\alpha, n, l, m) = \alpha \cdot \dfrac{l + 1}{l+m+2} + (1-\alpha) \cdot \dfrac{l + 1}{l+n+2}

The idea is that the more things in l the more similar the two clauses are.

• sf(\alpha, n, l m) tends to 0: no limits to popssioble differences
• sf(\alpha, n, l, m) tends to 1: identity
• sf(\alpha, n, l, m) = 0.5: maximum uncertainty

Why don’t we use other similarity measures like dice, jaccard, etc? Because they assign 1 in many ways, while we want to assign 1 only for identity.

How do we apply this similarity? For object we can extract 2 features: position and properties and we represent clause as a Directed Acyclic Graph, where nodes are literals and edges are at least one shared term. So the level 0 of the tree is the head, in the next level there is the new literals linked with last velel and incoming edge form each linked node of previous level. Leaves are nodes with no outgoing edges.

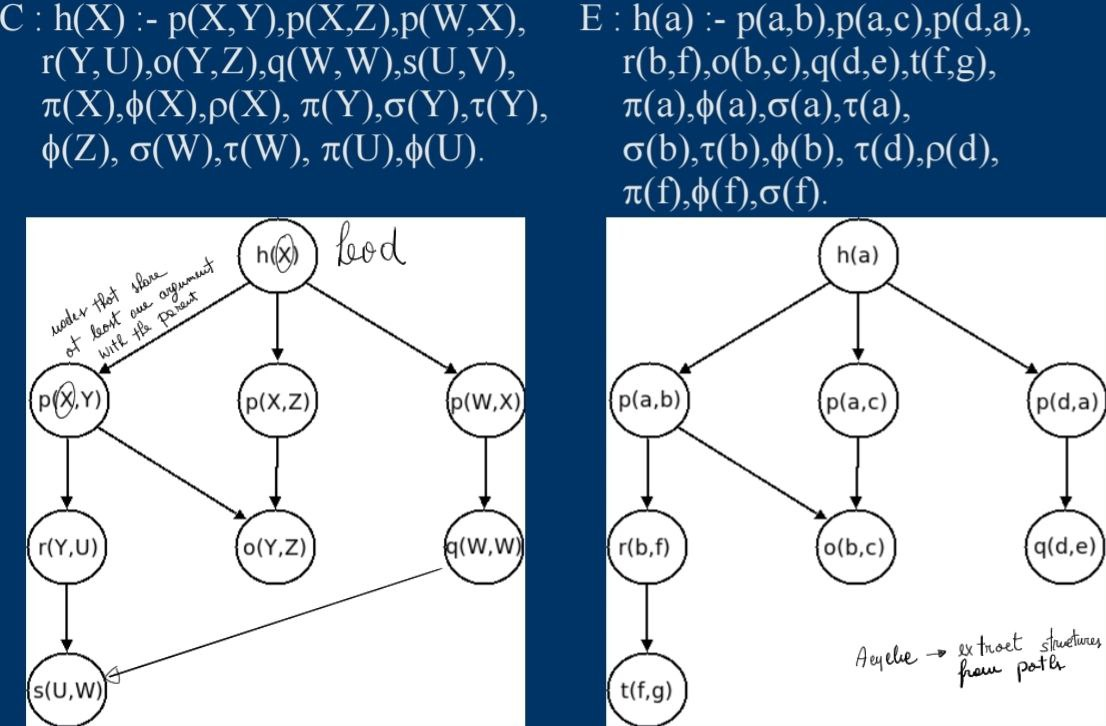
So the process is:

1. Extract all paths root-leaf
2. Compute the similarity

The similarity in a path is the literal similarity until compatible literals are found (using least general generalization).