2 Ontologies
There are some problems in knowledge representation. For example, at what level to represent knowledge and which properties of objects are so basic that they are present in all domains. Additionally, there are primitives to which all knowledge can be reduced and whether it is possible to obtain new knowledge. Modeling for conceptualization requires specific and dedicated activities to make explicit the knowledge that was previously implicit. The ontology defines the type of things that exist in the application domain.
An ontology is the study of the existence of all kinds of entities that make up the world. It aims at providing a framework of distinctions that can be used to discriminate and classify things that exist and define words that describe them. The idea is to model explicit knowledge in a way that can be shared and reused.
In philosophy, we talk about the theory of a priori distinctions applicable independently of the state of the world between particulars, that are, the physical entities in the world (objects, quantity of matter, events, …) and universals, that are, the meta-level categories used to model the world (concepts, properties, qualities, …).
In Computer Science, ontologies are used to improve communication among people and organizations:
- To foster system interoperability, sharing modeling methods, paradigms, languages and software tools.
- To support IT systems engineering, fostering reusability through the sharing of formal representations.
- Improving search, using metadata to index information systems.
- Expressing specifications, helping the identification of the requirements of an IT system.
- To support knowledge management, providing a common vocabulary for the domain.
The first step in the design of databases, knowledge bases and OOP systems is the selection of ontological categories: what can be represented in a family of applications. Any incompleteness or restriction in the structure of categories limits the generality of all programs or databases using them.
2.1 Ontology definition
We have several definitions of ontology, each of them brings a different perspective on the concept:
- Philosophy: “a systematic explanation of being”
- Neches: “…defines the basic terms and relations including the vocabulary of a topic area as well as the rules for combining terms and relations to define extensions to the vocabulary”
- Gruber, the most cited: “… an explicit specification of a conceptualization”
- Borst: “…a formal specification of a shared conceptualization”
- Guarino: “…a logical theory which gives an explicit, partial account of a conceptualization”
Gruber introduces the explicit term, which brings the aim of communication, and of conceptualization, that is, identifying the relevant things we want to describe, identifying their properties and behaviors, and describing them. Borst introduces the term shared: a community should first of all agree on a conceptualization. Guarino introduces the concept of partial account: we cannot capture all the complexity of the world, but only a meaningful subset. In general, the definitions agree on the formal and systematic nature of an ontology; in particular, Guarino talks about a logical theory.
In the end, we can define an ontology as follows: an ontology is a formal conceptualization of the world, expressed by a set of rules representing the structure of a specific aspect of reality, and including formulas that can be considered as always being true and thus can be shared by several agents independently of the particular state of things.
Given an ontology, a legal description of the world is any possible world that satisfies the constraints.
A formal ontology is an explicit and formal description of the conceptualization of a domain in terms of concepts, properties of the concepts, and semantic relationships among them. More in detail: an axiomatic first-order theory that can be expressed in a Description Logic.
2.2 Relationships
Defining inter-relationships among categories helps us in structuring our conceptual system.
The main ontological relationships are:
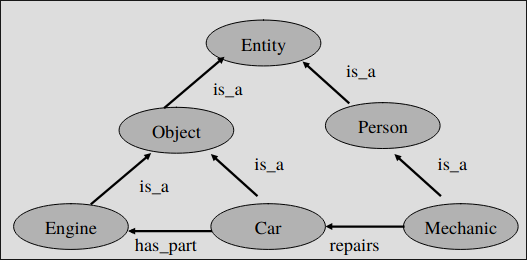
- Hyponymy or inclusion between classes. This kind of relation brings the concepts of generalization/specialization and hierarchies/heterarchies.
- is_a relationships allow reasoning by inheritance; for instance, if Cat is_a Pet, all features of pets are also features of cats. The transitive property is valid: if Cat is_a Pet and Pet is_a Animal, then Cat is_a Animal.
- instance_of relationships (between instances and categories)
- Meronymy between entities, intended as whole and its part.
- part_of relationships: apply to objects made up of sets of components; for instance, Paw part_of Cat. All these relationships establish partial orderings within the domain, but instead of storing all the relationships explicitly, only first-level ones are stored, and a mechanism is provided to generate the others as needed.
- Troponymy between verbs and processes, that is, a hyponymy for verbs: verb v1 is a troponym of v2 if v1 indicates a specific case of the more generic v2 (e.g., falling is a troponym of moving).
In the context of taxonomic relationships we can distinguish between:
- Taxonomic relations, that is, the relation between a class and its subclasses (is-a-kind-of). It’s a special type of hyponymy and it vertically structures taxonomic hierarchies, or heterarchies if multiple inheritance is allowed.
- Inclusion relationships: the relation between a class and its instances, widely exploited in defining any kind of conceptual structure that tries to capture the intuition of humans, which suggests the existence of natural categories of hyponyms. It is a horizontal structuring of the domain; that is, it defines the relations between classes and instances.
2.3 Hierarchies of Ontologies
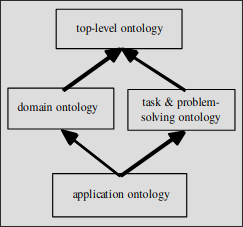
Top-level foundational ontologies: the aim is to simplify the design of domain-specific ontologies, improving quality and understandability by representing a rigorous context for comparisons, evaluation, and choices, enforcing the reuse of ontologic resources. They are very abstract, defining concepts like Person, Event, Time, Space, PhysicalObject, etc. They are not domain-specific but are used to define domain ontologies.
Domain ontologies: they are used to represent the knowledge of a specific domain.
Task ontologies: they are used to represent the knowledge of a specific task.
Application ontologies: they are used to represent the knowledge of a specific application.
A lexical ontology like WordNet defines a given number of concepts that represent the meaning of words in a language. They tend to a “generalization of common sense”.
The use of an ontology may improve reasoning and retrieval activities, while its structure supports the browsing activity.
2.4 Formal ontology
The 3 components are the set of concepts (classes), the relationships among them, and a logic level that allows inferring new facts from those encoded within the resource. The latter is optional if we talk about a simple taxonomy.
Formally, we have a triple O = (C, R, A), where C is a set of concepts, R is a set of conceptual relationships each defined over C \times C, and A is a set of axioms. If A = \emptyset, the ontology is not axiomatized (that is, it is a taxonomy). C and R induce a graph G = (V, E), where nodes represent concepts and arcs represent relationships, with a labeling function for arcs to distinguish relations from each other.
O’ = (C’, R’, A’)
- C’ = {Entity, Object, Person, Mechanic, Car, Engine}
- R’ = { is_a, has, repairs }
- is_a = { (Object, Entity), (Person, Entity), (Mechanic, Person), (Car, Object), (Engine, Object) }
- has_part = { (Car, Engine) }
- repairs = { (Mechanic, Car) }
- A’ = { “\foralla \in Car : \existsm \in Mechanic: repairs(m, a)” }
2.5 Ontological Language
The language used for an ontology can be simple (concepts only), frame-based, or logic-based (OWL), in order to design (consistency check), integrate (assert relationships), and use (determine whether a fact is consistent with respect to the ontology) an ontology. To do so, we use a description language that is simpler than First-Order Logic languages to obtain better computational properties, involving only atomic concepts, roles (binary relationships), and names of objects (individuals).
The main features with respect to First-Order Logic are the following:
- Unique Names Assumption is not supported: different names may denote the same concept; we can later state that they are the same concepts with a same_as relation.
- Open World Assumption: not knowing a fact does not necessarily mean it is false, but it means that it is unknown. First-Order Logic follows a Closed World Assumption.
Each description logic is characterized by operators to build two kinds of terms: concepts, corresponding to unary relationships, and roles, corresponding to binary relationships. Individuals are used only in assertions.
One famous description logic language is OWL, a markup language to explicitly represent the meaning and semantics of terms through vocabularies and relationships among them.
The ontology is divided into two boxes: T-Box (TBox) and A-Box (ABox).
The T-Box contains the terminological knowledge of a domain, that is, the basic concepts and the relationships among them. It represents intensional knowledge: it defines subsumption relationships between concepts and allows classifying them in an inheritance hierarchy. We can think of the T-box as a lattice1 with a top and a bottom.
The T-Box is a set of axioms that define the vocabulary of the ontology.
The A-Box contains the assertional knowledge, that is, the facts about individuals (the extensional knowledge).
The A-Box is a set of assertions that describe the instances of the concepts defined in the T-Box. An A-Box satisfies a T-Box if it respects all the constraints in the T-Box.
2.5.1 T-Box
The T-Box is a set of axioms that defines the vocabulary of the ontology. It contains the definitions of the concepts and the relationships among them. The T-Box is used to classify the concepts and to infer new knowledge from the existing knowledge.
The symbols used in the T-Box are:
- inclusion of concepts:
- C1 \sqsubseteq C2: C1 is a subclass of C2
- C1 \sqsupseteq C2: C1 is a superclass of C2
- inclusion of roles:
- R1 \sqsubseteq R2: R1 is a subrole of R2
- R1 \sqsupseteq R2: R1 is a superrole of R2
- equality of concepts
- C1 \equiv C2: C1 is equivalent to C2
- equality of roles
- R1 \equiv R2: R1 is equivalent to R2
The set of instances satisfies the T-Box if it respects all the constraints in the T-Box.
Basic symbols appear only on the right-hand side, while defined symbols also appear on the left-hand side but only once. We assume the set of axioms to be acyclic because we need it for the expansion: acyclic terminologies can be expanded by replacing defined symbols with their definitions.
2.5.2 A-Box
An A-Box is a set of assertions of 2 kinds:
- a:C is an assertion about concepts, a^{I} \in C^{I}
- (b,c):R is an assertion about roles, (b^{I}, c^{I}) \in R^{I}
a, b, c, d are meta-symbols for individuals. I also provide an interpretation for the symbols of individuals.
2.5.3 DLs as Fragments of FOL
Assertions in Description Logics can be translated into FOL formulas through the definition of a translation function t(C, x) \rightarrow C(x), that returns a FOL formula with x as a free variable.
A lattice is a partially ordered set in which every pair of elements has a unique least upper bound (supremum) and greatest lower bound (infimum). In ontologies, this structure helps organize concepts hierarchically.↩︎